题目内容
12.给出以下四个结论:①函数$f(x)=\frac{2x-1}{x+1}$的对称中心是(-1,2);
②若关于x的方程$x-\frac{1}{x}+k=0在x∈({0,1})$没有实数根,则k的取值范围是k≥2;
③在△ABC中,“bcosA=acosB”是“△ABC为等边三角形”的充分不必要条件;
④若$f(x)=sin({2x-\frac{π}{3}})$的图象向右平移φ(φ>0)个单位后为奇函数,则φ最小值是$\frac{π}{12}$.
其中正确的结论是①.
分析 根据函数图象平移变换法则,可判断①;判断x∈(0,1)时,x$-\frac{1}{x}$的范围,可判断②;根据充要条件的定义,可判断③;根据正弦型函数的对称性和奇偶性,可判断④.
解答 解:①函数$f(x)=\frac{2x-1}{x+1}$=$\frac{-3}{x+1}$+2,其图象由反比例函数y=$\frac{-3}{x}$的图象向左平移两单位,再向上平移2个单位得到,故图象的对称中心是(-1,2),故①正确;
②x∈(0,1)时,x$-\frac{1}{x}$∈(-∞,0),若关于x的方程$x-\frac{1}{x}+k=0在x∈({0,1})$没有实数根,则k的取值范围是k≥0,故②错误;
③在△ABC中,“bcosA=acosB”?“sinBcosA=sinAcosB”?“sin(A-B)=0”?“A=B”⇒“△ABC为等腰三角形”,“bcosA=acosB”是“△ABC为等边三角形”的必要不充分条件,故③错误;
④若$f(x)=sin({2x-\frac{π}{3}})$的图象向右平移φ(φ>0)个单位后为奇函数,-2φ-$\frac{π}{3}$=kπ,k∈Z,
当k=-1时,φ最小值是$\frac{π}{3}$,故④错误;
故答案为:①
点评 本题以命题的真假判断与应用为载体,考查了函数的对称性,方程的根,函数的值域,充要条件,正弦型函数的图象和性质,难度中档.

练习册系列答案
相关题目
5.已知直线l的参数方程为:$\left\{\begin{array}{l}{x=2t}\\{y=1+4t}\end{array}\right.$(t为参数),圆C的极坐标方程为$ρ=2\sqrt{2}sinθ$,则直线l与圆C的位置关系为( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无法确定 |
7.4名同学甲、乙、丙、丁按任意次序站成一排,甲或乙站在边上的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
17.在等腰直角△ABC中,∠ABC=90°,AB=BC=2,M,N(不与A,C重合)为AC边上的两个动点,且满足|$\overrightarrow{MN}$|=$\sqrt{2}$,则$\overrightarrow{BM}$•$\overrightarrow{BN}$的取值范围为( )
| A. | [$\frac{3}{2}$,2] | B. | ($\frac{3}{2}$,2) | C. | [$\frac{3}{2}$,2) | D. | [$\frac{3}{2}$,+∞) |
4.某小组有7人,现在从任选3人相互调整位置,其余4人位置不变,则不同调整方案有( )种.
| A. | 35 | B. | 70 | C. | 210 | D. | 105 |
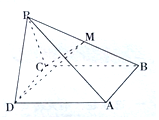 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.