题目内容
10.设函数$f(x)=\frac{a}{x^2}+lnx,a∈R$.(1)讨论函数f(x)的单调性;
(2)如果对任意的$x∈[{\frac{1}{2},2}]$,都有$f(x)≥\frac{1}{x}$恒成立,求实数a的取值范围.
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)问题等价于当x∈[$\frac{1}{2}$,2]时,a≥x-x2lnx恒成立,记H(x)=x-x2lnx,根据函数的单调性求出H(x)的最大值,从而求出a的范围即可.
解答 解:(1)f′(x)=-$\frac{2a}{{x}^{3}}$+$\frac{1}{x}$=$\frac{{x}^{2}-2a}{{x}^{3}}$,(x>0),
a≤0时,f′(x)>0,函数f(x)在(0,+∞)递增,
a>0时,令f′(x)>0,得x>$\sqrt{2a}$,即函数f(x)的递增区间是($\sqrt{2a}$,+∞),
令f′(x)<0,解得:0<x<$\sqrt{2a}$,
即函数f(x)的递减区间是(0,$\sqrt{2a}$);
(2)问题等价于当x∈[$\frac{1}{2}$,2]时,a≥x-x2lnx恒成立,
记H(x)=x-x2lnx,∴a≥H(x)max,H′(x)=1-2xlnx-x,H′(1)=0,
令m(x)=1-2xlnx-x,∴m′(x)=-3-2lnx,
由于x∈[$\frac{1}{2}$,2],m′(x)=-3-2lnx<0,
∴m(x)=1-2xlnx-x在[$\frac{1}{2}$,2]递减,
x∈[$\frac{1}{2}$,1]时,H′(x)>0,x∈(1,2]时,H′(x)<0,
即函数H(x)=x-x2lnx在区间[$\frac{1}{2}$,1]递增,在区间(1,2]递减,
∴H(x)max=H(1)=1,从而a≥1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
相关题目
5.已知直线l的参数方程为:$\left\{\begin{array}{l}{x=2t}\\{y=1+4t}\end{array}\right.$(t为参数),圆C的极坐标方程为$ρ=2\sqrt{2}sinθ$,则直线l与圆C的位置关系为( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无法确定 |
17.在等腰直角△ABC中,∠ABC=90°,AB=BC=2,M,N(不与A,C重合)为AC边上的两个动点,且满足|$\overrightarrow{MN}$|=$\sqrt{2}$,则$\overrightarrow{BM}$•$\overrightarrow{BN}$的取值范围为( )
| A. | [$\frac{3}{2}$,2] | B. | ($\frac{3}{2}$,2) | C. | [$\frac{3}{2}$,2) | D. | [$\frac{3}{2}$,+∞) |
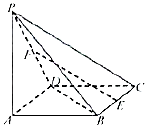 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA=AB=2,$PB=2\sqrt{2}$,$PC=2\sqrt{3}$,E,F分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA=AB=2,$PB=2\sqrt{2}$,$PC=2\sqrt{3}$,E,F分别为BC,PD的中点.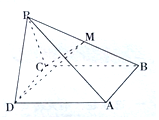 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.