题目内容
已知椭圆C:
+y2=1经过点P(1,
).
(Ⅰ)求椭圆C的方程及其离心率;
(Ⅱ)过椭圆右焦点F的直线(不经过点P)与椭圆交于A、B两点,当∠APB的平分线为PF时,求直线AB的斜率k.
| x2 |
| a2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程及其离心率;
(Ⅱ)过椭圆右焦点F的直线(不经过点P)与椭圆交于A、B两点,当∠APB的平分线为PF时,求直线AB的斜率k.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用椭圆C:
+y2=1经过点P(1,
),求出a,可得求椭圆C的方程及其离心率;
(Ⅱ)记PA、PB的斜率分别为k1、k2.所以,PA、PB的斜率满足k1+k2=0,设直线AB方程为y=k(x-1),代入椭圆方程,利用韦达定理进行计算,即可求直线AB的斜率k.
| x2 |
| a2 |
| ||
| 2 |
(Ⅱ)记PA、PB的斜率分别为k1、k2.所以,PA、PB的斜率满足k1+k2=0,设直线AB方程为y=k(x-1),代入椭圆方程,利用韦达定理进行计算,即可求直线AB的斜率k.
解答:
解:(Ⅰ)把点P(1 ,
)代入
+y2=1,可得a2=2.
故椭圆的方程为
+y2=1,
所以c=1,椭圆的离心率为e=
. …(4分)
(Ⅱ)由(Ⅰ)知:F(1,0).
当∠APB的平分线为PF时,由P(1 ,
)和F(1,0)知:PF⊥x轴.
记PA、PB的斜率分别为k1、k2.所以,PA、PB的斜率满足k1+k2=0…(6分)
设直线AB方程为y=k(x-1),代入椭圆方程
+y2=1并整理可得,(1+2k2)x2-4k2x+2(k2-1)=0.
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
又P(1 ,
),则k1=
=
=
+k,k2=
=
=
+k.…(8分)
所以k1+k2=
+
=
+
-
•
=2k-
•
=2k-
…(11分)
即2k-
=0.
所以k=
. …(13分)
| ||
| 2 |
| x2 |
| a2 |
故椭圆的方程为
| x2 |
| 2 |
所以c=1,椭圆的离心率为e=
| 1 | ||
|
(Ⅱ)由(Ⅰ)知:F(1,0).
当∠APB的平分线为PF时,由P(1 ,
| ||
| 2 |
记PA、PB的斜率分别为k1、k2.所以,PA、PB的斜率满足k1+k2=0…(6分)
设直线AB方程为y=k(x-1),代入椭圆方程
| x2 |
| 2 |
设A(x1,y1),B(x2,y2),则x1+x2=
| 4k2 |
| 1+2k2 |
| 2(k2-1) |
| 1+2k2 |
又P(1 ,
| ||
| 2 |
| ||||
| 1-x1 |
| ||||
| 1-x1 |
| ||||
| 1-x1 |
| ||||
| 1-x2 |
| ||||
| 1-x2 |
| ||||
| 1-x2 |
所以k1+k2=
| ||||
| 1-x1 |
| ||||
| 1-x2 |
| y1 |
| x1-1 |
| y2 |
| x2-1 |
| ||
| 2 |
| x1+x2-2 |
| x1x2-(x1+x2)+1 |
| ||
| 2 |
| ||||
|
| 2 |
即2k-
| 2 |
所以k=
| ||
| 2 |
点评:本题考查椭圆的基本知识,直线和椭圆的位置关系等知识点,解题时要认真审题,仔细解答,合理地进行等价转化.

练习册系列答案
相关题目
甲乙丙三位同学独立的解决同一个问题,已知三位同学能够正确解决这个问题的概率分别为
、
、
,则有人能够解决这个问题的概率为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
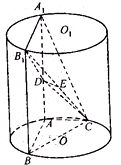 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.