题目内容
已知a,b,c∈R,且a+b+c=3,a2+b2+c2的最小值为M.
(Ⅰ)求M的值;
(Ⅱ)解关于x的不等式|x+4|-|x-1|≥M.
(Ⅰ)求M的值;
(Ⅱ)解关于x的不等式|x+4|-|x-1|≥M.
考点:二维形式的柯西不等式,绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)由柯西不等式可得(a2+b2+c2)(1+1+1)≥(a+b+c)2=9,从而求得a2+b2+c2的最小值为M.
(Ⅱ)把不等式|x+4|-|x-1|≥3等价转化为与之等价的三个不等式组,求得每个不等式组的解集,再取并集,即得所求.
(Ⅱ)把不等式|x+4|-|x-1|≥3等价转化为与之等价的三个不等式组,求得每个不等式组的解集,再取并集,即得所求.
解答:
解:(Ⅰ)由柯西不等式可得(a2+b2+c2)(1+1+1)≥(a+b+c)2=9,
故a2+b2+c2 ≥3,即a2+b2+c2的最小值为M=3.
(Ⅱ)由不等式|x+4|-|x-1|≥3,可得
①,或
②,或
③.
解①求得 x∈∅,解②求得 0≤x<1,解③求得x≥1,
综上可得,不等式的解集为[0,+∞).
故a2+b2+c2 ≥3,即a2+b2+c2的最小值为M=3.
(Ⅱ)由不等式|x+4|-|x-1|≥3,可得
|
|
|
解①求得 x∈∅,解②求得 0≤x<1,解③求得x≥1,
综上可得,不等式的解集为[0,+∞).
点评:本题主要考查二维形式的柯西不等式的应用,绝对值不等式的解法,体现了等价转化和分类讨论的数学思想,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
已知点P在抛物线y2=8x上,那么点P到点Q(3,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
A、(
| ||
B、(
| ||
C、(3,2
| ||
| D、(3,-2) |
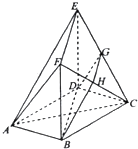 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE,CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE,CF的中点.