题目内容
9.设x,y满足约束条件$\left\{\begin{array}{l}{x-y≤0}\\{x+2y-6≤0}\\{2x+y-3≥0}\end{array}\right.$,目标函数z=ax-y仅在(0,3)取得最大值,则a的取值范围是( )| A. | ($\frac{1}{2}$,+∞) | B. | (-2,-$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$) | D. | (-∞,-2) |
分析 先画出满足条件的平面区域,将z=ax-y转化为y=ax-z,由图象得直线仅在(0,3)取得最大值,只需直线y=ax-z的斜率小于直线2x+y-1=0的斜率即可,从而求出a的范围.
解答 解:画出满足条件的平面区域,如图示: ,
,
由z=ax-y,得:y=ax-z,
由图象得直线仅在(0,3)取得最大值,
只需直线y=ax-z的斜率小于直线2x+y-1=0的斜率即可,
∴a<-2,
故选:D.
点评 本题考察了简单的线性规划问题,考察数形结合思想,是一道基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
19.下列从集合A到集合B的对应f是映射的是( )
| A. | A=R,B={x|x是正实数},f:A中的数的绝对值 | |
| B. | A={0,1},B={-1,0,1},f:A中的数的开方 | |
| C. | A=Z,B=Q,f:A中的数的倒数 | |
| D. | A={-1,0,1},B={-1,0,1},f:A中的数的平方 |
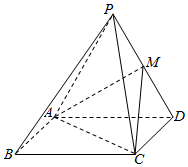 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,且△PAD是边长为4的正三角形,M为PD的中点,底面ABCD是矩形,CD=3.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,且△PAD是边长为4的正三角形,M为PD的中点,底面ABCD是矩形,CD=3. 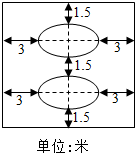 某学校拟在广场上建造一个矩形花园,如图所示,中间是完全相同的两个椭圆型花坛,每个椭圆型花坛的面积均为216π平方米,两个椭圆花坛的距离是1.5米.整个矩形花坛的占地面积为S.
某学校拟在广场上建造一个矩形花园,如图所示,中间是完全相同的两个椭圆型花坛,每个椭圆型花坛的面积均为216π平方米,两个椭圆花坛的距离是1.5米.整个矩形花坛的占地面积为S.