题目内容
14.设函数f(x)=$\left\{\begin{array}{l}{2^{-x}}-1,{\;}^{\;}x≤0\\{x^{\frac{1}{2}}},{\;}^{\;}{\;}^{\;}x>0\end{array}$如果f(x0)>1,则x0的取值范围是( )| A. | (-1,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
分析 根据分段函数的表达式,进行求解即可.
解答 解:若x0>0,由f(x0)>1得${{x}_{0}}^{\frac{1}{2}}$=$\sqrt{{x}_{0}}$>1得x0>1,
若x0≤0,由f(x0)>1得${2}^{-{x}_{0}}$-1>1得${2}^{-{x}_{0}}$>2,
即-x0>1,则x0<-1,
综上x0>1或x0<-1,
故选:C
点评 本题主要考查不等式的求解,根据分段函数的表达式进行讨论求解即可.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
9.若函数f(x)=x3-ax在x=2处取得极小值,则a=( )
| A. | 6 | B. | 12 | C. | 2 | D. | -2 |
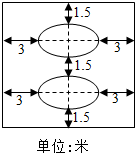 某学校拟在广场上建造一个矩形花园,如图所示,中间是完全相同的两个椭圆型花坛,每个椭圆型花坛的面积均为216π平方米,两个椭圆花坛的距离是1.5米.整个矩形花坛的占地面积为S.
某学校拟在广场上建造一个矩形花园,如图所示,中间是完全相同的两个椭圆型花坛,每个椭圆型花坛的面积均为216π平方米,两个椭圆花坛的距离是1.5米.整个矩形花坛的占地面积为S.