题目内容
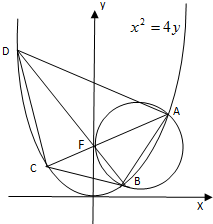 已知抛物线G:x2=4y;
已知抛物线G:x2=4y;(Ⅰ)过点P(2,1)作抛物线G的切线,求切线方程;
(Ⅱ)设A(x1,y1),B(x2,y2)是抛物线G上异于原点的两动点,其中x1>x2>0,以A,B为直径的圆恰好过抛物线的焦点F,延长AF,BF分别交抛物线G于C,D两点,若四边形ABCD的面积为32,求直线AC的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)设出直线方程,联立直线和抛物线方程,利用判别式等于0求解斜率,则切线方程可求;
(2)由题意可设直线AC的方程为y=kx+1(k≠0),得到BD的方程,分别和抛物线联立后利用弦长公式求得AC,BD的长度,代入四边形的面积公式求得直线斜率,则直线AC的方程可求.
(2)由题意可设直线AC的方程为y=kx+1(k≠0),得到BD的方程,分别和抛物线联立后利用弦长公式求得AC,BD的长度,代入四边形的面积公式求得直线斜率,则直线AC的方程可求.
解答:
解:(1)由题意可知,抛物线的切线的斜率存在,设为k(k≠0),
过点P(2,1)的切线方程为y-1=k(x-2),
联立
,得x2-4kx+4(2k-1)=0.
由△=0,即16k2-16(2k-1)=0,解得k=1.
∴所求的直线方程是y=x-1;
(2)由题意可设直线AC的方程为y=kx+1(k≠0),
则直线BD的方程为y=-
x+1.
由
,得x2-4kx-4=0.
∴x1+x2=4k,x1x2=-4.
∴|AC|=
|x1-x2|=
=4(1+k2).
同理:|BD|=4×(1+
)=
.
∵四边形ABCD的面积为32,
∴
|AC||BD|=32,
即
×4(1+k2)×
=32.
解得:k=1或k=-1.
∴直线AC的方程是:y=x+1.
过点P(2,1)的切线方程为y-1=k(x-2),
联立
|
由△=0,即16k2-16(2k-1)=0,解得k=1.
∴所求的直线方程是y=x-1;
(2)由题意可设直线AC的方程为y=kx+1(k≠0),
则直线BD的方程为y=-
| 1 |
| k |
由
|
∴x1+x2=4k,x1x2=-4.
∴|AC|=
| 1+k2 |
| 1+k2 |
| 16k2+16 |
同理:|BD|=4×(1+
| 1 |
| k2 |
| 4(1+k2) |
| k2 |
∵四边形ABCD的面积为32,
∴
| 1 |
| 2 |
即
| 1 |
| 2 |
| 4(1+k2) |
| k2 |
解得:k=1或k=-1.
∴直线AC的方程是:y=x+1.
点评:本题考查了直线和圆锥曲线的关系,训练了判别式法求曲线的切线方程,考查了弦长公式的应用,涉及直线与曲线的关系问题,常采用直线与圆锥曲线联立,根据方程的根与系数的关系求解,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是压轴题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
水面直径为0.2m的鱼缸的水面上飘着一块面积为0.02m2的浮萍,则向鱼缸随机撒鱼食时,鱼食掉在浮萍上的概率为( )
| A、0.1 | ||
| B、0.02 | ||
| C、0.2 | ||
D、
|
两条平行直线和圆的位置关系定义为:若两条平行直线和圆有4个不同的公共点,则称两条平行直线和圆“相交”;若两条平行直线和圆没有公共点,则称两条平行直线和圆“相离”;若两条平行直线和圆有1个、2个或3个不同的公共点,则称两条平行直线和圆“相切”.已知直线l1:2x-y+a=0,l2:2x-y+a2+1=0和圆:x2+y2+2x-4=0相切,则a的取值范围是( )
A、-3≤a≤-
| ||||
B、a>
| ||||
| C、a>7或 a<-3 | ||||
| D、a≥7或 a≤-3 |