题目内容
假设数学测验的成绩都是正整数，甲、乙两人某次数学测验成绩都是两位正整数，且十位数字都是8，求甲、乙两人此次数学成绩的差的绝对值不超过2的概率．（画图解答）
考点：列举法计算基本事件数及事件发生的概率
专题：概率与统计
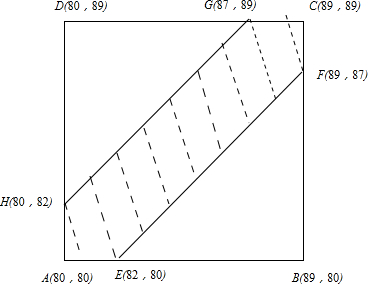
分析：设甲的成绩为x，乙的成绩为y，则（x，y）对应如图所示的正方形ABCD及其内部的整数点，其中满足|x-y|≤2的（x，y）对应的点如图阴影部分（含边界）的整数点，问题得以解决
解答：
解：设甲的成绩为x，乙的成绩为y，x，y∈{80，81，82，••，89}，
则（x，y）对应如图所示的正方形ABCD及其内部的整数点，共有10×10=100，
其中满足|x-y|≤2的（x，y）对应的点如图阴影部分（含边界）的整数点，共有100-7×8=44，
故所求概率为P=
=
，
解：设甲的成绩为x，乙的成绩为y，x，y∈{80，81，82，••，89}，则（x，y）对应如图所示的正方形ABCD及其内部的整数点，共有10×10=100，
其中满足|x-y|≤2的（x，y）对应的点如图阴影部分（含边界）的整数点，共有100-7×8=44，
故所求概率为P=
| 44 |
| 100 |
| 11 |
| 25 |
点评：本题考查了概率公式的计算，关键是画出图象，属于中档题
练习册系列答案
相关题目
已知椭圆E：
+
=1（a＞b＞0）的右顶点为A（a，0），离心率为
，过点A的直线交椭圆于另一点B，若AB的中点坐标为（1，-
），则E的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
为了了解某种产品的质量，抽取容量为30的样本，检测结果为一级品5件，二级品8件．三级品13件，其余的部是次品．已知样本频率分布表的一部分如图所示：
函数