Question

2013年某时刻，在钓鱼岛附近的海岸A处发现北偏东45°方向，距A处（

3

-1）海里的B处有一艘日本走私船，在A处北偏西75°方向，距A处2海里的C处的中国巡逻舰，奉命以10

3

海里/时的速度追截日本走私船，此时日本走私船正以10海里/时的速度，从B处向北偏东30°方向逃窜．问：中国巡逻舰沿什么方向行驶才能最快截获日本走私船？并求出所需时间．（改编题）

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：设缉私船追上走私船需t小时，进而可表示出CD和BD，进而在△ABC中利用余弦定理求得BC，进而在△BCD中，根据正弦定理可求得sin∠BCD的值，进而求得∠BDC=∠BCD=30°进而求得BD，进而利用BD=10t求得t．

解答： 解：如图所示，设缉私船追上走私船需t小时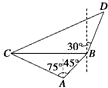，则有CD=10

3

t，BD=10t．
在△ABC中，
∵AB=

3

-1，AC=2，
∠BAC=45°+75°=120°．
根据余弦定理可求得BC=

( 3 -1)2+22-2×( 3 -1)×2×(- 1 2 )

=

6

．
∠CBD=90°+30°=120°．
在△BCD中，根据正弦定理可得
sin∠BCD=

10t•sin120°

10 3 t

=

1

2

，
∵∠CBD=120°，∴∠BCD=30°，∠BDC=30°，
∴BD=BC=

6

，则有10t=

6

，t=

6

10

（小时）．
∴缉私船沿北偏东60°方向，需

6

10

小时才能追上走私船．

点评：本题主要考查了解三角形的实际应用．考查了运用三角函数的基础知识解决实际的问题．