题目内容
在△ABC中，已知2cos（B+C）=1，b+c=3
，bc=4，求：
（1）角A的度数；
（2）边a的长度．
| 3 |
（1）角A的度数；
（2）边a的长度．
考点：正弦定理,余弦定理
专题：解三角形
分析：（1）△ABC中，由条件根据2cos（B+C）=1，求得cosA的值，可得A的值．
（2）由条件利用余弦定理求得a的值．
（2）由条件利用余弦定理求得a的值．
解答：
解：（1）△ABC中，∵已知2cos（B+C）=1=-2cosA，∴cosA=-
，A=120°．
（2）由余弦定理可得a2=b2+c2-2bc•cosA=（b+c）2-2bc+bc=27-4=23，
∴a=
．
| 1 |
| 2 |
（2）由余弦定理可得a2=b2+c2-2bc•cosA=（b+c）2-2bc+bc=27-4=23，
∴a=
| 23 |
点评：本题主要考查诱导公式、余弦定理的应用，属于基础题．
练习册系列答案
相关题目
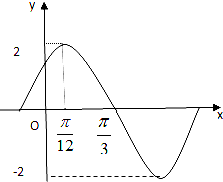已知函数f（x）=Acos（ωx+φ），（A＞0，ω＞0，|φ|＜