题目内容

6．已知等差数列{an}的首项a2=5，前4项和S4=28．
（1）求数列{an}的通项公式；
（2）若bn=（-1）nan，求数列{bn}的前2n项和T2n．

分析 （1）利用等差数列的通项公式及其前n项和公式即可得出．
（2）分组求和即可得出．

解答 解：（1）由已知条件：$\left\{\begin{array}{l}{a_2}={a_1}+d=5\\{S_4}=4{a_1}+\frac{4×3}{2}×d=28\end{array}\right.$，
∴$\left\{\begin{array}{l}{a_1}=1\\ d=4.\end{array}\right.$，
∴an=a1+（n-1）×d=4n-3．
（2）由（1）可得${b_n}={（-1）^n}{a_n}={（-1）^n}（{4n-3}）$，
T2n=-1+5-9+13-17+…+（8n-3）=4×n=4n．

点评 本题考查了等差数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
3．从集合A={2，3，-4}中随机选取一个数记为k，则函数y=kx为单调递增的概率为（　　）
A．$\frac{2}{9}$B．$\frac{1}{3}$C．$\frac{4}{9}$D．$\frac{2}{3}$
4．设f（x）为一多项式，若（x+1）f（x）除以x2+x+1的余式为5x+3，则f（x）除以x2+x+1的余式为2x+5．
14．已知点A（0，-1），B（3，0），C（1，2），平面区域P是由所有满足$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$（2＜λ≤m，2＜μ≤n）的点M组成的区域，若区域P的面积为6，则m+n的最小值为4+$\sqrt{3}$．
1．已知单调递增的等比数列{an}满足：a2+a3+a4=28，且a3+2是a2、a4的等差中项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若bn=anlog2an，Sn=b1+b2+…+bn，求数列{bn}的前n项和Sn．
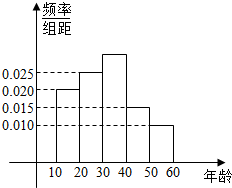11．某市在“国际禁毒日”期间，连续若干天发布了“珍爱生命，原理毒品”的电视公益广告，期望让更多的市民知道毒品的危害性，禁毒志愿者为了了解这则广告的宣传效果，随机抽取了100名年龄阶段性在[10，20），[20，30），[30，40），[40，50），[50，60）的市民进行问卷调查，由此得到样本频率分布直方图如图所示．
（Ⅰ）求随机抽取的市民中年龄段在[30，40）的人数；
（Ⅱ）从不小于40岁的人中按年龄段分层抽样的方法随机抽取5人，求[50，60）年龄段抽取的人数；
（Ⅲ）从（Ⅱ）中方式得到的5人中再抽取2人作为本次活动的获奖者，记X为年龄在[50，60）年龄段的人数，求X的分布列及数学期望．
18．下列函数中，在其定义域内是增函数而且又是奇函数的是（　　）
A．y=2xB．y=2|x|C．y=2x-2-xD．y=2x+2-x
15．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{b}$|=4，$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是$\frac{1}{2}$，则$\overrightarrow{a}$•$\overrightarrow{b}$=2．
16．已知数列{an}的前n项和为Sn，a1=1，Sn=2an+1，则当n＞1时，Sn=（　　）
A．（$\frac{3}{2}$）n-1B．2n-1C．（$\frac{2}{3}$）n-1D．$\frac{1}{3}$（$\frac{1}{{2}^{n-1}}$-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网