Question

14．已知点A（0，-1），B（3，0），C（1，2），平面区域P是由所有满足$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$（2＜λ≤m，2＜μ≤n）的点M组成的区域，若区域P的面积为6，则m+n的最小值为4+$\sqrt{3}$．

Answer 1

分析 设M（x，y），作出M点所在的平面区域，根据面积得出关于m，n的等式，利用基本不等式便可得出m+n的最小值．

解答 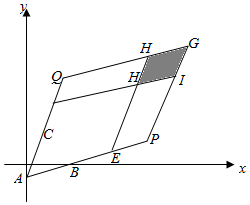解：设M（x，y），$\overrightarrow{AB}=（3，1），\overrightarrow{AC}=（1，3）$，$|\overrightarrow{AB}|=|\overrightarrow{AC}|=\sqrt{10}$；
∴$cos＜\overrightarrow{AB}，\overrightarrow{AC}＞=\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}=\frac{3+3}{10}=\frac{3}{5}$，$sin＜\overrightarrow{AB}，\overrightarrow{AC}＞=\frac{4}{5}$；
令$\overrightarrow{AE}=2\overrightarrow{AB}，\overrightarrow{AF}=2\overrightarrow{AC}$，以AE，AF为邻边作平行四边形AENF，令$\overrightarrow{AP}=m\overrightarrow{AB}，\overrightarrow{AQ}=n\overrightarrow{AC}$，以AP，AQ为邻边作平行四边形APGQ；
∵$\overrightarrow{AM}=λ\overrightarrow{AB}+μ\overrightarrow{AC}（2＜λ≤m，2＜μ≤n）$；
∴符合条件的M组成的区域是平行四边形NIGH，如图所示；
∴$（m-2）\sqrt{10}•（n-2）\sqrt{10}•\frac{4}{5}=6$；
∴$（m-2）（n-2）=\frac{3}{4}$；
∵$（m-2）（n-2）≤\frac{（m+n-4）^{2}}{4}$；
∴$\frac{3}{4}≤\frac{（m+n-4）^{2}}{4}$；
∴3≤（m+n-4）²；
∴$m+n≥4+\sqrt{3}$；
∴m+n的最小值为$4+\sqrt{3}$．
故答案为：4+$\sqrt{3}$．

点评 本题考查了平面向量的几何意义，向量加法的平行四边形法则，以及三角形的面积公式，基本不等式，根据区域面积得出关于m，n的关系是解题关键．