题目内容
15.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{b}$|=4,$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是$\frac{1}{2}$,则$\overrightarrow{a}$•$\overrightarrow{b}$=2.分析 设$\overrightarrow{a},\overrightarrow{b}$的夹角为θ,则|$\overrightarrow{a}$|cosθ=$\frac{1}{2}$,于是$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=4×$\frac{1}{2}$=2.
解答 解:设$\overrightarrow{a},\overrightarrow{b}$的夹角为θ,则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为|$\overrightarrow{a}$|cosθ=$\frac{1}{2}$,∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=4×$\frac{1}{2}$=2.
故答案为:2.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
7.微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,将男性、女性使用微信的时间分成5组:(0,2],(2,4],(4,6],(6,8],(8,10]分别加以统计,得到如图所示的频率分布直方图.
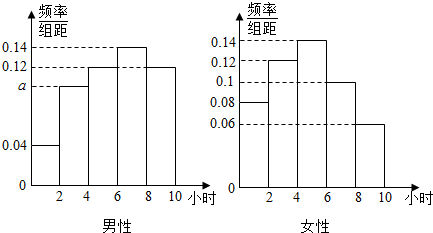
(Ⅰ)根据女性频率直方图估计女性使用微信的平均时间;
(Ⅱ)若每天玩微信超过4小时的用户列为“微信控”,否则称其为“非微信控”,
请你根据已知条件完成2×2的列联表,并判断是否有90%的把握认为“微信控”与“性别”有关?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:

(Ⅰ)根据女性频率直方图估计女性使用微信的平均时间;
(Ⅱ)若每天玩微信超过4小时的用户列为“微信控”,否则称其为“非微信控”,
请你根据已知条件完成2×2的列联表,并判断是否有90%的把握认为“微信控”与“性别”有关?
| 微信控 | 非微信控 | 合计 | |
| 男性 | 50 | ||
| 女性 | 50 | ||
| 合计 | 100 |
参考数据:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5.若sinα=2cosα,则$\frac{sinα-cosα}{sinα+cosα}$的值为( )
| A. | 1 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | -1 |