Question

11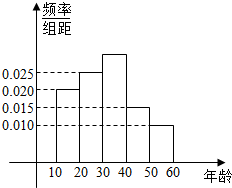．某市在“国际禁毒日”期间，连续若干天发布了“珍爱生命，原理毒品”的电视公益广告，期望让更多的市民知道毒品的危害性，禁毒志愿者为了了解这则广告的宣传效果，随机抽取了100名年龄阶段性在[10，20），[20，30），[30，40），[40，50），[50，60）的市民进行问卷调查，由此得到样本频率分布直方图如图所示．
（Ⅰ）求随机抽取的市民中年龄段在[30，40）的人数；
（Ⅱ）从不小于40岁的人中按年龄段分层抽样的方法随机抽取5人，求[50，60）年龄段抽取的人数；
（Ⅲ）从（Ⅱ）中方式得到的5人中再抽取2人作为本次活动的获奖者，记X为年龄在[50，60）年龄段的人数，求X的分布列及数学期望．

Answer 1

分析 （I）由频率分布直方图求出随机抽取的市民中年龄段在[30，40）的频率，由此能求出随机抽取的市民中年龄段在[30，40）的人数．
（II）由频率分布直方图得不小于40岁的人的频数是25人，由此能求出在[50，60）年龄段抽取的人数．
（III）由已知X=0，1，2，分别求出相应的概率，由此能求出X的分布列及数学期望．

解答 解：（I）由频率分布直方图知，随机抽取的市民中年龄段在[30，40）的频率为：
1-10×（0.020+0.025+0.015+0.010）=0.3，
即随机抽取的市民中年龄段在[30，40）的人数为100×0.3=30人．  …（3分）
（II）由（I）知，年龄段在[40，50），[50，60）的人数分别为100×0.15=15人，100×0.1=10人，
即不小于40岁的人的频数是25人，
∴在[50，60）年龄段抽取的人数为10×$\frac{5}{25}$=2人． …（6分）
（III）由已知X=0，1，2，
P（X=0）=$\frac{C_3^2}{C_5^2}=\frac{3}{10}$，
P（X=1）=$\frac{C_2^1C_3^1}{C_5^2}=\frac{3}{5}$，
P（X=2）=$\frac{C_2^2}{C_5^2}=\frac{1}{10}$，
∴X的分布列为

X	0	1	2
P	$\frac{3}{10}$	$\frac{3}{5}$	$\frac{1}{10}$

∴EX=0×$\frac{3}{10}$+1×$\frac{3}{5}$+2×$\frac{1}{10}$=$\frac{4}{5}$． …（12分）

点评 本题考查频率分布直方图、排列组合、相互独立事件的概率和随机变量分布列和数学期望等概念，同时考查学生的逻辑思维能力和分析问题及解决问题的能力．