题目内容
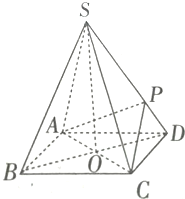 如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱长都是底面边长的
如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱长都是底面边长的| 2 |
(1)求证:SO⊥平面ABCD;
(2)若SD⊥平面PAC,求直线SB与平面PAC所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)直接利用题中的已知条件,利用线面垂直的判定定理求出结论.
(2)首先利用三角形的中位线,把线面的夹角进行转化,进一步利用线段的长求出所构成的直角三角形的边长,最后通过解三角形求得结果.
(2)首先利用三角形的中位线,把线面的夹角进行转化,进一步利用线段的长求出所构成的直角三角形的边长,最后通过解三角形求得结果.
解答:
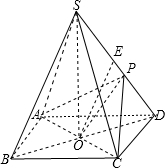 证明:(1)四棱锥S-ABCD的底面是正方形,每条侧棱长都是底面边长的
证明:(1)四棱锥S-ABCD的底面是正方形,每条侧棱长都是底面边长的
倍,
所以所有的侧棱长都相等.
即:SB=SD=SA=SC,O为底面ABCD的交点
所以:AO=CO,BO=BO
则:SO⊥AC,SO⊥BD
所以:SO⊥平面ABCD
(2)设底面边长为x,则侧棱长为
x,
利用勾股定理得:DO=
x,
取SD的中点E,
所以:OE∥SB
且OE=
SB=
x,
在Rt△SOD中,SO2+OD2=SD2
解得:SO=
x,
由于:SD⊥平面PAC
所以:PO⊥SD
利用三角形面积相等:OP•SD=SO•OD
解得:OP=
x
所以:cos∠EOP=
=
则:∠EOP=
由于OE∥SB,所以直线SB与平面PAC所成角即为OE与平面PAC所成角.
直线OE与平面PAC所成角为
,所以:直线SB与平面PAC所成角为
.
所以直线SB与平面PAC所成夹角的正弦值为
.
 证明:(1)四棱锥S-ABCD的底面是正方形,每条侧棱长都是底面边长的
证明:(1)四棱锥S-ABCD的底面是正方形,每条侧棱长都是底面边长的| 2 |
所以所有的侧棱长都相等.
即:SB=SD=SA=SC,O为底面ABCD的交点
所以:AO=CO,BO=BO
则:SO⊥AC,SO⊥BD
所以:SO⊥平面ABCD
(2)设底面边长为x,则侧棱长为
| 2 |
利用勾股定理得:DO=
| ||
| 2 |
取SD的中点E,
所以:OE∥SB
且OE=
| 1 |
| 2 |
| ||
| 2 |
在Rt△SOD中,SO2+OD2=SD2
解得:SO=
| ||
| 2 |
由于:SD⊥平面PAC
所以:PO⊥SD
利用三角形面积相等:OP•SD=SO•OD
解得:OP=
| ||
| 4 |
所以:cos∠EOP=
| OE |
| OP |
| ||
| 2 |
则:∠EOP=
| π |
| 6 |
由于OE∥SB,所以直线SB与平面PAC所成角即为OE与平面PAC所成角.
直线OE与平面PAC所成角为
| π |
| 6 |
| π |
| 6 |
所以直线SB与平面PAC所成夹角的正弦值为
| 1 |
| 2 |
点评:本题考查的知识要点:线面垂直的判定,勾股定理得应用,线面的夹角问题的应用,及相关的运算问题.属于基础题型.

练习册系列答案
相关题目
若θ∈[0,
],sin2θ=
,则cosθ=( )
| π |
| 4 |
2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
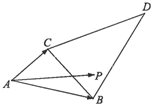
如图,△BCD与△ABC的面积之比为2,点P是区域ABCD内任意一点(含边界),且
=λ
+μ
(λ,μ∈R),则λ+μ的取值范围是( )
| AP |
| AB |
| AC |

| A、[0,1] |
| B、[0,2] |
| C、[0,3] |
| D、[0,4] |
已知函数f(x)=2x3-3ax2+8,若f(x)存在唯一的零点x0,且x0<0,则实数a的取值范围是( )
| A、(-∞,0) |
| B、(-∞,0)∪[2,+∞) |
| C、[0,2] |
| D、(-∞,2) |