题目内容
8.设椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A、右焦点为F,B为椭圆E在第二象限上的点,直线BO交椭圆E于点C,若直线BF平分线段AC,则椭圆E的离心率是$\frac{1}{3}$.分析 设AC中点为M,连接OM,则OM为△ABC的中位线,运用三角形的中位线定理和三角形相似的性质可得离心率.
解答  解:如图,设AC中点为M,连接OM,
解:如图,设AC中点为M,连接OM,
则OM为△ABC的中位线,
于是△OFM∽△AFB,且$\frac{|OF|}{|FA|}$=$\frac{|OM|}{|AB|}$=$\frac{1}{2}$,
即$\frac{c}{a-c}$=$\frac{1}{2}$可得e=$\frac{c}{a}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查椭圆的方程和性质,主要是离心率的求法,运用中位线定理和三角形相似的性质是解题的关键.

练习册系列答案
相关题目
2.下面几个空间图形中,虚线、实线使用不正确的有( )
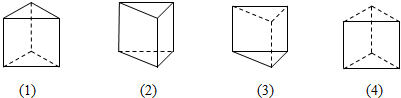

| A. | (2)(3) | B. | (1)(3) | C. | (3)(4) | D. | (4) |
3. 如图是一个程序框图,则输出的n的值是( )
如图是一个程序框图,则输出的n的值是( )
 如图是一个程序框图,则输出的n的值是( )
如图是一个程序框图,则输出的n的值是( )| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左焦点为F,过点F的直线交椭圆于A,B两点,|AF|的最大值为M,|BF|的最小值为m,满足$M•m=\frac{3}{4}{a^2}$.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左焦点为F,过点F的直线交椭圆于A,B两点,|AF|的最大值为M,|BF|的最小值为m,满足$M•m=\frac{3}{4}{a^2}$.