题目内容
18.已知定义在R上的函数f(x),g(x)满足$\frac{f(x)}{g(x)}={a^x}$,且f′(x)g(x)<f(x)g′(x),$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{5}{2}$,若有穷数列$\left\{{\frac{f(n)}{g(n)}}\right\},n∈{N^*}$的前n项和为$\frac{255}{256}$,则n=8.分析 由f′(x)g(x)<f(x)g′(x)可知y=ax时减函数,结合$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{5}{2}$可解出a,从而得出数列的通项公式,带入求和公式即可解出n的值.
解答 解:令F(x)=$\frac{f(x)}{g(x)}={a^x}$,
则F′(x)=$\frac{f′(x)g(x)-f(x)g′(x)}{(g(x))^{2}}$<0,
∴F(x)=$\frac{f(x)}{g(x)}={a^x}$是减函数,
∴0<a<1
∵$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{5}{2}$,
∴a+$\frac{1}{a}$=$\frac{5}{2}$,
∴a=$\frac{1}{2}$.
∴{$\frac{f(n)}{g(n)}$}=($\frac{1}{2}$)n.
其前n项和为Sn=1-($\frac{1}{2}$)n.
∴1-($\frac{1}{2}$)n=$\frac{255}{256}$,
解得n=8.
故答案为:8.
点评 本题考查了函数单调性与导数的关系及数列求和,属于综合题.

练习册系列答案
相关题目
9.已知幂函数y=f(x)的图象过点$({3,\sqrt{3}})$,则log2f(2)的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | -1 |
6.设F1,F2是双曲线$\frac{x^2}{8}-{y^2}$=1的两个焦点,点P在双曲线上,且∠F1PF2=90°,则点P到x轴的距离为( )
| A. | $\sqrt{7}$ | B. | 3 | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{7}}}{7}$ |
13.已知数列{an}的其前n项和Sn=n2-6n,则数列{|an|}前10项和为( )
| A. | 58 | B. | 56 | C. | 50 | D. | 45 |
7.已知f(x)+f(1-x)=2,an=f(0)+f($\frac{1}{n}$)+…+f($\frac{n-1}{n}$)+f(1)(n∈N*),则数列{an}的通项公式为( )
| A. | an=n-1 | B. | an=n | C. | an=n+1 | D. | an=n2 |
8. 阅读程序框图,若输出的$y=\frac{1}{2}$,则输入的x的值可能为( )
阅读程序框图,若输出的$y=\frac{1}{2}$,则输入的x的值可能为( )
 阅读程序框图,若输出的$y=\frac{1}{2}$,则输入的x的值可能为( )
阅读程序框图,若输出的$y=\frac{1}{2}$,则输入的x的值可能为( )| A. | -1 | B. | 0 | C. | 5 | D. | 1 |
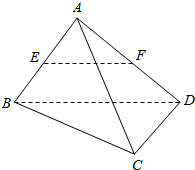 在空间四边形ABCD中,E,F分别是AB,AD的中点
在空间四边形ABCD中,E,F分别是AB,AD的中点