某三棱锥的三视图如图所示.则该三棱锥的体积是( )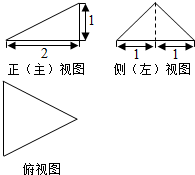A．$\frac{2}{3}$B．2C．$\sqrt{3}$D．$\frac{{\sqrt{3}}}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

13．某三棱锥的三视图如图所示，则该三棱锥的体积是（　　）

A．

$\frac{2}{3}$

B．

C．

$\sqrt{3}$

D．

$\frac{{\sqrt{3}}}{3}$

分析棱锥的底面积为俯视图三角形的面积，棱锥的高为1，代入体积公式计算即可．

解答解：由三视图可知几何体为三棱锥，棱锥的底面为俯视图三角形，面积为S=$\frac{1}{2}×2×2$=2，棱锥的高h=1，
∴棱锥的体积V=$\frac{1}{3}$Sh=$\frac{1}{3}×2×1$=$\frac{2}{3}$．
故选A．

点评本题考查了棱锥的三视图和体积计算，属于基础题．

练习册系列答案

4．

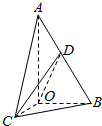如图，在Rt△AOB中，∠OAB=30°，斜边AB=4，将△AOB绕直线AO旋转得到△AOC，且二面角B-AO-C是直二面角，动点D在边AB上．
（Ⅰ）求证：平面COD⊥平面AOB；
（Ⅱ）当D为AB的中点时，求异面直线AO与CD所成角的正切值；
（Ⅲ）求CD与平面AOB所成角的正切值的最大值．

1．

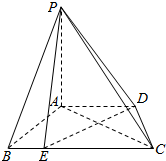如图，在四棱锥P-ABCD中，PA⊥面ABCD，AB⊥AD，BC∥AD，AP=$\sqrt{2}$，AB=AD=1，BC=2，$\overrightarrow{BE}=\frac{1}{4}\overrightarrow{BC}$．
（I）求证：平面PAC⊥平面PDE
（II）求直线PC与平面PDE所成角的正弦值．

8．已知棱长为2，各面均为等边三角形的四面体，则其表面积为（　　）

$\frac{4}{3}\sqrt{3}$

18．已知α，β是两个不同的平面，m，n是两条不同的直线，给出下列命题：
①若m⊥α，m?β，则α⊥β；
②若m⊥n，m⊥α，则n∥α；
③若α∩β=m，n∥m，且n?α，n?β，则n∥α且n∥β．
④若m∥α，α⊥β，则m⊥β．
其中真命题的个数是（　　）

5．某几何体的三视图如图所示，则该几何体的表面积为（　　）

2．设数列{a_n}的前n项和为S_n，且a₁=1，a_n+1=2S_n+3，则S₄=66．

3．设a=log₃7，b=2^1.1，c=0.8^3.1，则（　　）

试题分类