题目内容
已知数列{an}满足an+1=
,a1=2,求an.
| 2n+1•an |
| an+2n+1 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由题意转化为出
-
=2n+1,再利用累加法求出通项,问题得以解决
| 1 |
| an+1 |
| 1 |
| an |
解答:
解:∵an+1=
,
∴an+1(an+2n+1)=an•2n+1,
∴an+1•an=(an-an+1)2n+1,
∴
-
=2n+1,
∴
-
=2,
-
=22,
…,
-
=2n,
两边累加得,
∴
-
=2+22+23+…+2n=
=2n+1-2,
∴
=2n+1-
,
∴an=
| 2n+1•an |
| an+2n+1 |
∴an+1(an+2n+1)=an•2n+1,
∴an+1•an=(an-an+1)2n+1,
∴
| 1 |
| an+1 |
| 1 |
| an |
∴
| 1 |
| a2 |
| 1 |
| a1 |
| 1 |
| a3 |
| 1 |
| a2 |
…,
| 1 |
| an |
| 1 |
| an-1 |
两边累加得,
∴
| 1 |
| an |
| 1 |
| 2 |
| 2(1-2n) |
| 1-2 |
∴
| 1 |
| an |
| 3 |
| 2 |
∴an=
| 2 |
| 2n+2-3 |
点评:本题考查数列的递推式求和通项的问题,关键求出
-
=2n+1,利用累加法求出通项的常用方法,属于中档题
| 1 |
| an+1 |
| 1 |
| an |

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
若集合A={x|log2x<0},集合B={x|(
)x≤1},则A∩B=( )
| 1 |
| 2 |
| A、{x|0<x<1} |
| B、{x|0≤x<1} |
| C、∅ |
| D、{x|x>1} |
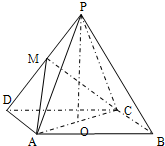 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC,O为AC中点,PO⊥平面ABCD,M为PD中点.若AC=2PO,求二面角P-AB-C的正切值.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC,O为AC中点,PO⊥平面ABCD,M为PD中点.若AC=2PO,求二面角P-AB-C的正切值.