题目内容
16.设函数f(x)=$\left\{{\begin{array}{l}{{x^3},0≤x<5}\\{f({x-5}),x≥5}\end{array}}$,那么f(2013)=27.分析 利用函数的周期性,以及函数的表达式求解即可.
解答 解:函数f(x)=$\left\{{\begin{array}{l}{{x^3},0≤x<5}\\{f({x-5}),x≥5}\end{array}}$,可知x≥5时,函数是周期为5的周期函数,
f(2013)=f(2010+3)=f(3)=33=27.
故答案为:27.
点评 本题考查分段函数的应用,函数的解析式求解函数值,考查转化思想以及计算能力.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
4.方程(a-1)x2+(2-a)y2=(a-1)(2-a)中,当1<a<2时,它表示( )
| A. | 椭圆或圆 | B. | 双曲线 | C. | 椭圆 | D. | 圆 |
4.已知a=log94,b=log64,c=$\frac{1}{2}$,则a,b,c的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
6.已知集合A={x|2x>1},集合B={x|x>m},则“m>0”是“A∪B=A”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
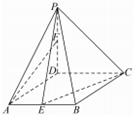 如图,在四棱锥P-ABCD中,∠BCD=60°,PD⊥平面ABCD,PD=AD=CD=1,点E、F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,∠BCD=60°,PD⊥平面ABCD,PD=AD=CD=1,点E、F分别为AB和PD的中点.