题目内容
11.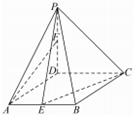 如图,在四棱锥P-ABCD中,∠BCD=60°,PD⊥平面ABCD,PD=AD=CD=1,点E、F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,∠BCD=60°,PD⊥平面ABCD,PD=AD=CD=1,点E、F分别为AB和PD的中点.(1)求证:直线AF∥平面PEC;
(2)求PC与平面PAB所成角的正弦值.
分析 (1)利用三角形中位线的性质证明线线平行,从而得到线面平行;
(2)根据直线间的两两垂直,尽力空间直角坐标系,再求出平面PAB的法向量,最后利用向量的数量积求出线面的夹角的正弦值.
解答 (1)证明:如图,
分别取PC,DC的中点G,H,连接FG,GH,EH,
则FG∥DH,FG=DH,DH∥AE,DH=AE,
∴FG∥AE,FG=AE,则四边形AEGF为平行四边形,则AF∥EG,
EG?平面PEC,AF?平面PEC,∴直线AF∥平面PEC; 解:∵底面ABCD是菱形,∠DAB=60°,点E、F分别为AB和PD中点,
解:∵底面ABCD是菱形,∠DAB=60°,点E、F分别为AB和PD中点,
∴DE⊥DC,
∵PD⊥平面ABCD,∴以D为原点,DE为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,
则 P(0,0,1),C(0,1,0),E($\frac{\sqrt{3}}{2}$,0,0),
A($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,0),B($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),
∴$\overrightarrow{AP}$=(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,1),$\overrightarrow{AB}$=(0,1,0).
设平面PAB的一个法向量为:$\overrightarrow{n}$=(x,y,z),.
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=y=0}\\{\overrightarrow{n}•\overrightarrow{AP}=-\frac{\sqrt{3}}{2}x+\frac{1}{2}y+z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,0,$\frac{\sqrt{3}}{2}$),
∵$\overrightarrow{PC}$=(0,1,-1),
∴设PC与平面PAB所成角为θ,
∴sinθ=$|\frac{\overrightarrow{PC}•\overrightarrow{n}}{|\overrightarrow{PC}||\overrightarrow{n}|}|$=$\frac{\sqrt{42}}{14}$.
∴PC平面PAB所成角的正弦值为$\frac{\sqrt{42}}{14}$.
点评 本题考查的知识要点:线面平行的判定的应用,空间直角坐标系的建立,法向量的应用,线面的夹角的应用,主要考查学生的空间想象能力和应用能力.

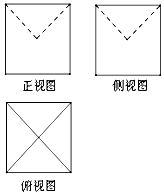 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )| A. | $8-\frac{π}{3}$ | B. | $8-\frac{π}{6}$ | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
| A. | [0,16] | B. | (0,16] | C. | (16,+∞) | D. | [16,+∞) |
| A. | 5 | B. | 1 | C. | 6 | D. | -2 |
| A. | (0,+∞) | B. | (-∞,0) | C. | (0,1] | D. | (-∞,1] |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | 6 | B. | -6 | C. | 2 | D. | -2 |
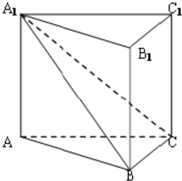 如图,在直三棱柱ABC-A1B1C1中,平面A1BC丄侧面A1AB B1,且 AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC丄侧面A1AB B1,且 AA1=AB=2.