题目内容
已知函数f(x)=
(sint-lgt)dt(x>1),则f(x)的极大值点的个数为( )
| ∫ | x 1 |
| A、0 | B、1 | C、2 | D、3 |
考点:定积分
专题:导数的概念及应用
分析:首先利用定积分求出函数f(x),然后再求导,绘制出导函数的图象,根据图象得出f(x)的单调区间,和f′(x)=0的点,继而求出函数的极值点.
解答:
解:f(x)=
(sint-lgt)dt=
[sint+ln10-[ln10-lgt)]dt=(-cost+ln10•t-tlgt)
=-cosx+ln10•x-xlnx+cos1-ln10
∴f′(x)=sinx-lgx,
绘制导函数的图象如图所示
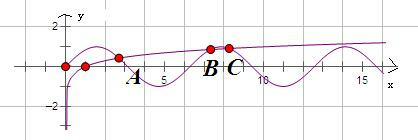
由图象可知当x在点A,B,C出sinx与lgx有交点,设交点横坐标分别为a,b,c
则当x=a,x=b,x=c时,f′(x)=0,
当f′(x)>0时,即在(0,a)或(b,c)函数f(x)为憎函数,
当f′(x)<0时,即在(a,b)或(c,+∞)函数f(x)为减函数,
故在x=a或x=c时函数f(x)有极大值.
故f(x)的极大值点的个数为2个.
故选:C.
| ∫ | x 1 |
| ∫ | x 1 |
| | | x 1 |
∴f′(x)=sinx-lgx,
绘制导函数的图象如图所示

由图象可知当x在点A,B,C出sinx与lgx有交点,设交点横坐标分别为a,b,c
则当x=a,x=b,x=c时,f′(x)=0,
当f′(x)>0时,即在(0,a)或(b,c)函数f(x)为憎函数,
当f′(x)<0时,即在(a,b)或(c,+∞)函数f(x)为减函数,
故在x=a或x=c时函数f(x)有极大值.
故f(x)的极大值点的个数为2个.
故选:C.
点评:本题主要考查了导数和函数的极值的问题,本题的关键是利用数形结合的思想,属于中档题.

练习册系列答案
相关题目
下列求导运算正确的是( )
A、(x+
| ||||
B、(log2x)′=
| ||||
| C、(3x)′=3xlog3e | ||||
| D、(x2cosx)′=-2xsinx |
已知命题p:?x0>0,lnx0<0.则¬p为( )
| A、?x>0,lnx≥0 |
| B、?x≤0,lnx≥0 |
| C、?x0>0,lnx0≥0 |
| D、?x0≤0,lnx0<0 |
求f(x)=
的定义域( )
| log2(-x2-5x+6) |
| x+2 |
| A、(-6,1) |
| B、(-∞,-6)∪(1,+∞) |
| C、(-6,-2)∪(-2,1) |
| D、R |
计算sin(-960°)的值为( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
若6名学生排成一列,则学生甲、乙、丙三人互不相邻的排位方法种数为( )
| A、24 | B、36 | C、72 | D、144 |
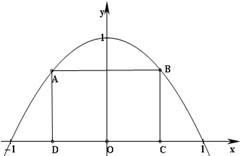 如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元.
如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元.