题目内容
设Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列,且a2+a5=2am,则m等于( )
| A、6 | B、7 | C、8 | D、10 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:先假设q=1,分别利用首项表示出前3、6、及9项的和,得到已知的等式不成立,矛盾,所以得到q不等于1,然后利用等比数列的前n项和的公式化简S3+S6=2S9得到关于q的方程,根据q不等于0和1,求出方程的解,即可得到q的值.然后求解m.
解答:
解:若q=1,则有S3=3a1,S6=6a1,S9=9a1.
但a1≠0,即得S3+S6≠2S9,与题设矛盾,q≠1.
又依题意S3+S6=2S9
可得
+
=
整理得q3(2q6-q3-1)=0.
由q≠0得方程2q6-q3-1=0.
(2q3+1)(q3-1)=0,
∵q≠1,q3-1≠0,
∴2q3+1=0
∴q3=-
,
a2+a5=2am,a2+a2q3=2a2qm-2.
∴
=2(-
)
,
∴m=8,
故选:C.
但a1≠0,即得S3+S6≠2S9,与题设矛盾,q≠1.
又依题意S3+S6=2S9
可得
| a1(1-q3) |
| 1-q |
| a1(1-q6) |
| 1-q |
| a1(1-q9) |
| 1-q |
整理得q3(2q6-q3-1)=0.
由q≠0得方程2q6-q3-1=0.
(2q3+1)(q3-1)=0,
∵q≠1,q3-1≠0,
∴2q3+1=0
∴q3=-
| 1 |
| 2 |
a2+a5=2am,a2+a2q3=2a2qm-2.
∴
| 1 |
| 2 |
| 1 |
| 2 |
| m-2 |
| 3 |
∴m=8,
故选:C.
点评:本小题主要考查等比数列的基础知识,逻辑推理能力和运算能力,是一道综合题.

练习册系列答案
相关题目
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.则f(20)等于( )


| A、761 | B、762 |
| C、841 | D、842 |
若5名学生排成一列,则其中学生甲站在最左边的排法种数为( )
| A、10 | B、48 | C、120 | D、24 |
利用数学归纳法证明不等式1+
+
+…+
<n(n≥2,n∈N)的过程中,进行第一步验证时,不等式左边应为( )之和.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
| A、1项 | B、2项 | C、3项 | D、4项 |
已知命题p:?x0>0,lnx0<0.则¬p为( )
| A、?x>0,lnx≥0 |
| B、?x≤0,lnx≥0 |
| C、?x0>0,lnx0≥0 |
| D、?x0≤0,lnx0<0 |
在△ABC中,设AD为BC边上的高,且AD=BC,b,c分别表示角B,C所对的边长,则
+
的取值范围是( )
| b |
| c |
| c |
| b |
A、[2,
| ||
B、[2,
| ||
C、[3,
| ||
D、[3,
|
求f(x)=
的定义域( )
| log2(-x2-5x+6) |
| x+2 |
| A、(-6,1) |
| B、(-∞,-6)∪(1,+∞) |
| C、(-6,-2)∪(-2,1) |
| D、R |
若6名学生排成一列,则学生甲、乙、丙三人互不相邻的排位方法种数为( )
| A、24 | B、36 | C、72 | D、144 |
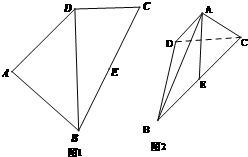 如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=
如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=