题目内容
19.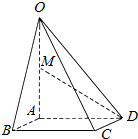 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.(1)求异面直线OC与MD所成角的正切值的大小;
(2)求点A到平面OBC的距离.
分析 (1)以A为原点,AB为x轴,AD为y轴,AO为z轴,建立空间直角坐标系,利用向量法能求出异面直线OC与MD所成角的正切值.
(2)求出平面OBC的法向量,利用向量法能求出点A到平面OBC的距离.
解答 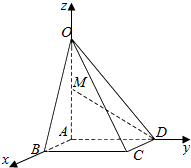 解:(1)以A为原点,AB为x轴,AD为y轴,AO为z轴,建立空间直角坐标系,
解:(1)以A为原点,AB为x轴,AD为y轴,AO为z轴,建立空间直角坐标系,
由题意O(0,0,2),C(2,2,0),M(0,0,1),D(0,2,0),
$\overrightarrow{OC}$=(2,2,-2),$\overrightarrow{MD}$=(0,2,-1),
设异面直线OC与MD所成角为θ,
则cosθ=$\frac{|\overrightarrow{OC}•\overrightarrow{MD}|}{|\overrightarrow{OC}|•|\overrightarrow{MD}|}$=$\frac{|6|}{\sqrt{12}•\sqrt{5}}$=$\frac{\sqrt{15}}{5}$,
∴tanθ=$\frac{{\sqrt{6}}}{3}$.
∴异面直线OC与MD所成角的正切值为$\frac{\sqrt{6}}{3}$.
(2)A(0,0,0),O(0,0,2),B(2,0,0),C(2,2,0)
$\overrightarrow{BA}$=(-2,0,0),$\overrightarrow{OB}$=(2,0,-2),$\overrightarrow{OC}$=(2,2,-2),
设平面OBC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{OB}=2x-2z=0}\\{\overrightarrow{n}•\overrightarrow{OC}=2x+2y-2z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,0,1),
∴点A到平面OBC的距离d=$\frac{|\overrightarrow{n}•\overrightarrow{BA}|}{|\overrightarrow{n}|}$=$\frac{|-2|}{\sqrt{2}}$=$\sqrt{2}$.
点评 本题考查异面直线所成角的求法,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.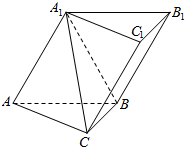 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°.
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°. 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2,点E位PC的中点
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2,点E位PC的中点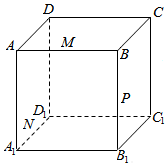 如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.
如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.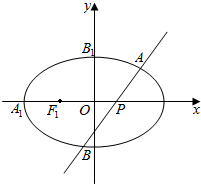 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,|A1B1|=$\sqrt{7}$,F1是椭圆C的左焦点,A1是椭圆C的左顶点,B1是椭圆C的上顶点,且$\overrightarrow{{A}_{1}{F}_{1}}$=$\overrightarrow{{F}_{1}O}$,点P(n,0)(n≠0)是长轴上的任一定点,过P点的任一直线l交椭圆C于A,B两点.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,|A1B1|=$\sqrt{7}$,F1是椭圆C的左焦点,A1是椭圆C的左顶点,B1是椭圆C的上顶点,且$\overrightarrow{{A}_{1}{F}_{1}}$=$\overrightarrow{{F}_{1}O}$,点P(n,0)(n≠0)是长轴上的任一定点,过P点的任一直线l交椭圆C于A,B两点.