题目内容

已知全集U=R，函数y=
1+x
+log3（4-x）的定义域为集合A．
（1）求集合A；
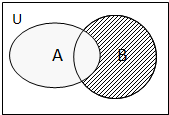
（2）集合B={x|2＜x≤10}，求韦恩图中阴影部分表示的集合C．
考点：对数函数的定义域,Venn图表达集合的关系及运算
专题：函数的性质及应用
分析：（1）由根式内部的代数式大于等于0，对数式的真数大于0求解不等式组得答案；
（2）阴影部分表示的集合C=（CUA）∩B，由交、补集运算得答案．
解答： 解：（1）由题得
x+1≥0
4-x＞0
，解得-1≤x＜4，
∴A={x|-1≤x＜4}；
（2）由韦恩图知阴影部分表示的集合C=（CUA）∩B，
又由（1）得CUA={x|x＜-1或x≥4}，
∴C=（CUA）∩B={x|x＜-1或x≥4}∩{x|2＜x≤10}={x|4≤x≤10}．
点评：本题考查了函数定义域的求法，考查了交集及其运算，关键是对图中阴影部分的表示，是基础题．
练习册系列答案
相关题目
已知双曲线
x2
6
-
y2
2
=1上任一点M（x0，y0），设M关于x轴对称点为M1，双曲线的左右顶点分别为A1，A2．
（Ⅰ）求直线A1M与直线A1M1的交点P的轨迹C的方程．
（Ⅱ）设点F（-2，0），T为直线x=-3上任意一点，过F作直线l⊥TF交（I）中轨迹C于P、Q两点，①证明：OT经过线段PQ中点（O为坐标原点）：②当
|TF|
|PQ|
最小时，求点T的坐标．
已知命题p：x∈R，f（x）=x2-2x+4＞m恒成立；q：f（x）=log5m-2x上的单调增函数．若p或q为真，p且q为假，求实数m的取值范围．
如图所示，为了测量某湖泊两侧A，B间的距离，李宁同学首先选定了与A，B不共线的一点C，然后给出了三种测量方案：（△ABC的角A，B，C所对的边分别记为a，b，c）：①测量A，C，b；②测量a，b，C；③测量A，a，b则一定能确定A，B间距离的所有方案的序号为（　　）
A、②③B、①②C、①③D、①②③
计算：
（1）0.25 
1
2
-[-2×（
3
7
）0]2×[（-2）3] 
4
3
+（
2
-1）-1-2 
1
2
；
（2）
2lg2+lg3
1+
1
2
lg0.36+
1
3
lg8
．
已知函数y=（
1
3
）|x|．
（1）求函数定义域；
（2）判断函数的奇偶性；
（3）画出函数图象，求函数的单调区间．
下列函数中，满足“对任意的x1，x2∈R，当x1＜x2时，都有f（x1）＜f（x2）”的是（　　）
A、y=log2x
B、y=-
1
x
C、y=2x
D、y=x2
圆锥的母线长为5，底面半径为3，则其体积为（　　）
A、15πB、30π
C、12πD、36π
已知椭圆C：
x2
a2
+
y2
b2
=1 (a＞b＞0)过点(
2
 ， 
3
3
)，且离心率为
6
3
，F1，F2为椭圆的左右焦点，直线l为椭圆的左准线，
（Ⅰ）求椭圆C的方程；
（Ⅱ）若点M在椭圆上，M到右焦点的距离为
3
-1，求点M到左准线l的距离．
（Ⅲ）若点P是椭圆C上的动点，PQ⊥l，垂足为Q，是否存在点P使得△F1PQ为等腰三角形，若存在，求出点P的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网