题目内容
在极坐标系中,已知曲线C1:ρ=2与曲线C2:ρsin(θ-
)=
交于不同的两点A,B,求AB的值.
| π |
| 4 |
| 2 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:利用
把极坐标方程化为直角坐标方程,再利用弦长公式即可得出.
|
解答:
解:曲线C1:ρ=2即ρ2=4,化为直角坐标方程为x2+y2=4,
曲线C2:ρsin(θ-
)=
展开为
ρ(sinθ-cosθ)=
,
化为直角坐标方程为x+y-2=0.
圆心到直线的距离d=
=
,
∴|AB|=2
=2
=2
.
曲线C2:ρsin(θ-
| π |
| 4 |
| 2 |
| ||
| 2 |
| 2 |
化为直角坐标方程为x+y-2=0.
圆心到直线的距离d=
| 2 | ||
|
| 2 |
∴|AB|=2
| r2-d2 |
| 4-2 |
| 2 |
点评:本题考查了极坐标方程化为直角坐标方程、直线与圆的相交问题、弦长公式、点到直线的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果执行图中的程序框图,那么最后输出的正整数i=( )


| A、43 | B、44 | C、45 | D、46 |
 甲、乙两位同学在相同的5次数学测试中,测试成绩如图所示,设
甲、乙两位同学在相同的5次数学测试中,测试成绩如图所示,设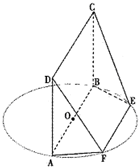 AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.
AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.