题目内容
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x,则当x∈[-3,0)时,f(x)的取值范围中( )
| A、[-3,0) |
| B、(0,1] |
| C、(0,3] |
| D、[-3,1] |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由于当x≥0时,f(x)=x2-2x=(x-1)2-1,利用二次函数的单调性可得x∈[0,3]时,f(x)∈[-1,3].
利用f(x)是定义在R上的奇函数,即可得出当x∈[-3,0)时,f(x)的取值范围.
利用f(x)是定义在R上的奇函数,即可得出当x∈[-3,0)时,f(x)的取值范围.
解答:
解:∵当x≥0时,f(x)=x2-2x=(x-1)2-1,
∴x∈[0,3]时,f(1)=-1,f(0)=0,f(3)=3,∴f(x)∈[-1,3].
∵f(x)是定义在R上的奇函数,
∴当x∈[-3,0)时,f(x)的取值范围是[-3,1].
故选:D.
∴x∈[0,3]时,f(1)=-1,f(0)=0,f(3)=3,∴f(x)∈[-1,3].
∵f(x)是定义在R上的奇函数,
∴当x∈[-3,0)时,f(x)的取值范围是[-3,1].
故选:D.
点评:本题考查了奇函数的性质,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
已知x,y满足
,则2x-y的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
一个四棱锥的三视图如图所示,其侧视图是等边三角形,该四棱锥的体积等于( )
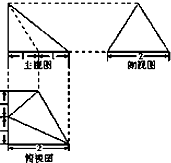

A、
| ||
B、2
| ||
C、3
| ||
D、6
|
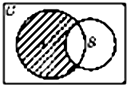 已知全集U=R,集合A={y|y=ln(x2+1),x∈R},集合A={x||x-2|≤1},则如图所示的阴影部分表示的集合为( )
已知全集U=R,集合A={y|y=ln(x2+1),x∈R},集合A={x||x-2|≤1},则如图所示的阴影部分表示的集合为( )| A、{x|0≤x<1或x>3} |
| B、{x|0≤x<1} |
| C、{x|x>3} |
| D、{x|1≤x≤3} |
已知集合A={x|x2-6x-7<0},B={x|x2+2x-8≥0},则A∪∁RB=( )
| A、{x|-1<x<7} |
| B、{x|x>2或x<-4 |
| C、{x|-1<x<2} |
| D、{x|-4<x<7} |
 已知函数y=6sin(ωx+ϕ)(ω>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若tan∠APB=2,则ω=
已知函数y=6sin(ωx+ϕ)(ω>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若tan∠APB=2,则ω=