题目内容

在递减等比数列{an}中，a1=27，若a1，a2，-3+a3成等差数列，则a5=
 
．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用a1，a2，-3+a3成等差数列，数列{an}是递减等比数列，求出公比，再求出a5．
解答： 解：∵a1，a2，-3+a3成等差数列，
∴2a2=a1-3+a3，
∴54q-24-27q2=0，
∵数列{an}是递减等比数列，
∴q=
2
3
，
∴a5=27•(
2
3
)4=
16
3
．
故答案为：
16
3
．
点评：本题考查等差数列的性质，考查等比数列的通项，考查学生的计算能力，确定公比是关键．
练习册系列答案
相关题目
若以直角坐标系的原点为极点，x轴的非负半轴为极轴建立极坐标系，则线段y=1-x（0≤x≤1）的极坐标方程为（　　）
A、ρ=
1
cosθ+sinθ
，0≤θ≤
π
2
B、ρ=
1
cosθ+sinθ
，0≤θ≤
π
4
C、ρ=cosθ+sinθ，0≤θ≤
π
2
D、ρ=cosθ+sinθ，0≤θ≤
π
4
己知数列{an}满足a1=1，a2n-a2n-1=2，a2n+1-a2n=3n（n∈N*）．
（I）计算：（a3-a1）+（a5-a3），并求a5；
（Ⅱ）求a2n-1（用含n的式子表示）；
（Ⅲ）记数列{an}的前n项和为Sn，求Sn．
函数f（x）=
-2x2+x+1
的定义域是
 
．
已知集合A={1，2，3，4}，B={m，3，6}，若A∩B={1，3}，则A∪B
 
．
已知a、b、c分别是△ABC的三个内角A，B，C所对的边，若a=1，b=
3
，∠B=60°，则AB=
 
．
设△ABC中，acosC，bcosB，ccosA成等差数列，则∠B=
 
．
函数f（x）=-x3-x+sinx，当θ∈（0，
π
2
）时，恒有f（cos2θ+2msinθ）+f（-2m-2）＞0成立，则实数m的取值范围（　　）
A、（-∞，
1
2
）
B、（-∞，
1
2
]
C、（-
1
2
，+∞）
D、[-
1
2
，+∞）
一个四棱锥的三视图如图所示，则此四棱至的四个侧面中的最大面积是（　　）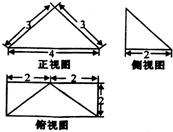
A、3
B、2
5
C、6
D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网