题目内容
已知某几何体的三视图如图所示,则该几何体的体积为 .


考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据几何体的三视图,得出该几何体是三棱锥,根据题目中的数据,求出该三棱锥的体积.
解答:
解:根据该几何体的三视图知,
该几何体是底面边长为2高为
的等腰三角形的三棱锥,
且三棱锥的高是
;
∴该三棱锥的体积是V=
×
×2×
×
=1.
故答案为:1.
该几何体是底面边长为2高为
| 3 |
且三棱锥的高是
| 3 |
∴该三棱锥的体积是V=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:1.
点评:本题考查了三视图的应用问题,解题时应把三视图还原为几何体,从而得出正确的答案,是基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
已知不重合的两条直线l,m和不重合的两个平面α,β,下列命题正确的是( )
| A、l∥m,l∥β,则m∥β |
| B、α∩β=m,l?α,则l∥β |
| C、α⊥β,l⊥α,则l∥β |
| D、l⊥m,m⊥β,l⊥α,则α⊥β |
 已知圆O:x2+y2=4,直线l:kx-y-k-1=0
已知圆O:x2+y2=4,直线l:kx-y-k-1=0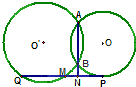 如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.
如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.