题目内容
已知函数f(x)=x2+2ax+4
(1)当a=-1时,求函数f(x)在区间[-2,2]上的最大值;
(2)若函数f(x)在区间[-1,3]上有零点,求实数a的取值范围.
(1)当a=-1时,求函数f(x)在区间[-2,2]上的最大值;
(2)若函数f(x)在区间[-1,3]上有零点,求实数a的取值范围.
考点:二次函数在闭区间上的最值,函数的零点
专题:函数的性质及应用
分析:(1)配方得f(x)=x2-2x+4=(x-1)2+3,根据性质得出最大值:f(-2)=12,
(2)分类讨论函数f(x)在区间[-1,3]上有且只有1个零点,函数f(x)在区间[-1,3]上有2个零点,根据函数性质的才不等式组求解即可.
(2)分类讨论函数f(x)在区间[-1,3]上有且只有1个零点,函数f(x)在区间[-1,3]上有2个零点,根据函数性质的才不等式组求解即可.
解答:
解:(1)∵当a=-1时,f(x)=x2-2x+4=(x-1)2+3,
∴函数f(x)在区间[-2,2]上的最大值:f(-2)=12,
(2)①函数f(x)在区间[-1,3]上有且只有1个零点,
(i)△=4a2-16=0,∴a=±2,
当a=2时,函数f(x)=x2-2x+4的零点为x=-2∉[-1,3],
当a=-2时,函数f(x)=x2-2x+4的零点为x=2∈[-1,3],
∴a=-2
(ii)当零点分别为-1,或3时,a的值分别为
或-
(ⅲ)f(-1)•f(3)<0,得(-2a+5)(6a+13)<0解得 a>
或a<-
②函数f(x)在区间[-1,3]上有2个零点,
,
解得:
即-
≤a<-2,
由①②得实数a的取值范围:a≤-2或a≥
∴函数f(x)在区间[-2,2]上的最大值:f(-2)=12,
(2)①函数f(x)在区间[-1,3]上有且只有1个零点,
(i)△=4a2-16=0,∴a=±2,
当a=2时,函数f(x)=x2-2x+4的零点为x=-2∉[-1,3],
当a=-2时,函数f(x)=x2-2x+4的零点为x=2∈[-1,3],
∴a=-2
(ii)当零点分别为-1,或3时,a的值分别为
| 5 |
| 2 |
| 13 |
| 6 |
(ⅲ)f(-1)•f(3)<0,得(-2a+5)(6a+13)<0解得 a>
| 5 |
| 2 |
| 13 |
| 6 |
②函数f(x)在区间[-1,3]上有2个零点,
|
解得:
|
| 13 |
| 6 |
由①②得实数a的取值范围:a≤-2或a≥
| 5 |
| 2 |
点评:本题综合考查了函数的性质,在解决函数零点问题中的应用,注意分类讨论,属于中档题.

练习册系列答案
相关题目
 如图,在正四面体A-BCD中,E为棱AD的中点,则CE与平面BCD的夹角的正弦值为( )
如图,在正四面体A-BCD中,E为棱AD的中点,则CE与平面BCD的夹角的正弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若一条直线与两个平行平面中的一个平面平行,则这条直线与另一个平面的位置关系是( )
| A、平行 | B、相交 |
| C、直线在平面内 | D、平行或直线在平面内 |
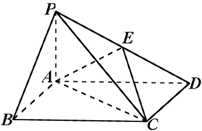 如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=3,且三棱锥E-ACD的体积为1.
如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=3,且三棱锥E-ACD的体积为1.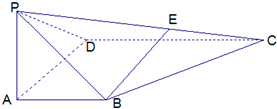
 如图所示,四棱锥P-ABCD的底面是直角梯形,PA⊥底面ABCD,AB⊥AD,CD⊥AD,CD=2AB,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD的底面是直角梯形,PA⊥底面ABCD,AB⊥AD,CD⊥AD,CD=2AB,E为PC的中点,PA=AD=AB=1.