题目内容
给出下列四个命题:
(1)若“p∧q”为假命题,则p,q均为假命题;
(2)若命题p:“?x∈R,x2-x-1>0”,则命题p的否定为:“?x∈R,x2-x-1≤0”;
(3)若x≠0,则x+
≥2;
(4)四个实数a,b,c,d依次成等比数列的必要而不充分条件是ad=bc.
正确命题的序号是 .
(1)若“p∧q”为假命题,则p,q均为假命题;
(2)若命题p:“?x∈R,x2-x-1>0”,则命题p的否定为:“?x∈R,x2-x-1≤0”;
(3)若x≠0,则x+
| 1 |
| x |
(4)四个实数a,b,c,d依次成等比数列的必要而不充分条件是ad=bc.
正确命题的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:(1)若“p∧q”为假命题,则p,q至少一个为假命题;
(2)利用命题的否定定义即可判断出;
(3)x<0时,x+
<0,不正确;
(4)四个实数a,b,c,d依次成等比数列⇒ad=bc,反之不成立,取c=d=0时.
(2)利用命题的否定定义即可判断出;
(3)x<0时,x+
| 1 |
| x |
(4)四个实数a,b,c,d依次成等比数列⇒ad=bc,反之不成立,取c=d=0时.
解答:
解:(1)若“p∧q”为假命题,则p,q至少一个为假命题,因此不正确;
(2)若命题p:“?x∈R,x2-x-1>0”,则命题p的否定为:“?x∈R,x2-x-1≤0”,正确;
(3)若x≠0,则x+
≥2,不正确,x<0时,x+
<0;
(4)四个实数a,b,c,d依次成等比数列的必要而不充分条件是ad=bc,正确.
综上可得:正确命题的序号是(2)(4).
故答案为:(2)(4).
(2)若命题p:“?x∈R,x2-x-1>0”,则命题p的否定为:“?x∈R,x2-x-1≤0”,正确;
(3)若x≠0,则x+
| 1 |
| x |
| 1 |
| x |
(4)四个实数a,b,c,d依次成等比数列的必要而不充分条件是ad=bc,正确.
综上可得:正确命题的序号是(2)(4).
故答案为:(2)(4).
点评:本题考查了简易逻辑的判定、等比数列的性质,考查了推理能力,属于基础题.

练习册系列答案
相关题目
如图,在正六边形ABCDEF中,
+
+
等于( )
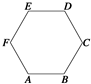
| BA |
| CD |
| FB |

| A、0 | ||
B、
| ||
C、
| ||
D、
|
 (1)如图所示的程序框图所表示的算法功能是什么?
(1)如图所示的程序框图所表示的算法功能是什么?