题目内容
一校办服装厂花费2万元购买某品牌运动装的生产与销售权,根据以往经验,每生产1百套这种品牌运动装的成本为1万元,每生产x(百套)的销售额R(x)(万元)满足:
R(x)=
(1)该服装厂生产750套此种品牌运动装可获得利润多少万元?
(2)该服装厂生产多少套此种品牌运动装利润最大?此时利润是多少万元?
R(x)=
|
(1)该服装厂生产750套此种品牌运动装可获得利润多少万元?
(2)该服装厂生产多少套此种品牌运动装利润最大?此时利润是多少万元?
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)根据利润=销售额R(x)-成本-2,将7.5代入,即可求出所求,注意单位互化;
(2)由题意,每生产x (百件)该品牌运动装的成本函数G(x)=x+2,利润函数f(x)=R(x)-G(x),然后分别求出每一段上的最大值,从而求出最大利润和生产的套数.
(2)由题意,每生产x (百件)该品牌运动装的成本函数G(x)=x+2,利润函数f(x)=R(x)-G(x),然后分别求出每一段上的最大值,从而求出最大利润和生产的套数.
解答:
解:(1)R(7.5)-1×7.5-2=3.2,(6分)
所以,生产750套此种品牌运动装可获得利润3.2 万元(1分)
(2)由题意,每生产x (百件)该品牌运动装的成本函数G(x)=x+2,
所以,利润函数f(x)=R(x)-G(x)=
当0<x≤5 时,f(x)=-0.4(x-4)2+3.6,(3分)
故当x=4 时,f(x) 的最大值为3.6. (1分)
当x>5 时,f(x)=9.7-[(x-3)+
]≤3.7,(3分)
故当x=6 时,f(x) 的最大值为3.7. (1分)
所以,生产600件该品牌运动装利润最大是3.7万元 (1分)
所以,生产750套此种品牌运动装可获得利润3.2 万元(1分)
(2)由题意,每生产x (百件)该品牌运动装的成本函数G(x)=x+2,
所以,利润函数f(x)=R(x)-G(x)=
|
当0<x≤5 时,f(x)=-0.4(x-4)2+3.6,(3分)
故当x=4 时,f(x) 的最大值为3.6. (1分)
当x>5 时,f(x)=9.7-[(x-3)+
| 9 |
| x-3 |
故当x=6 时,f(x) 的最大值为3.7. (1分)
所以,生产600件该品牌运动装利润最大是3.7万元 (1分)
点评:本题主要考查了函数模型的选择与应用,同时考查了分段函数的最值,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知函数f(x)在区间(0,a)上有唯一的零点(a>0),在用二分法寻找零点的过程中,依次确定了零点所在的区间为(0,
),(0,
),(0,
),则下列说法中正确的是( )
| a |
| 2 |
| a |
| 4 |
| a |
| 8 |
A、函数f(x)在区间(0,
| ||||||||
B、函数f(x)在区间(0,
| ||||||||
C、函数f(x)在(
| ||||||||
D、函数f(x)在区间(0,
|
(
+1)6(
-1)4的展开式中x的系数是( )
| x |
| x |
| A、-3 | B、3 | C、-4 | D、4 |
二项式(x2-
)6的展开式中不含x3项的系数之和为( )
| 2 |
| x |
| A、161 | B、159 |
| C、-161 | D、-159 |
定义域为R的函数f(x)满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x2-x,则当x∈(-1,0]时,f(x)的值域为( )
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[0,
|
已知a>1且实数x,y满足|x|+|y|≤1,则z=ax+y的最大值是( )
| A、1 | ||
| B、a+1 | ||
| C、a | ||
D、
|
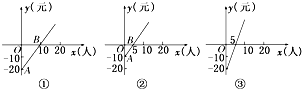 (函数的应用)如图①是某公共汽车线路收支差额y元与乘客量x的图象.
(函数的应用)如图①是某公共汽车线路收支差额y元与乘客量x的图象.