题目内容
 给定曲线Γ:(5-m)x2+(m-2)y2=8,(m∈R).
给定曲线Γ:(5-m)x2+(m-2)y2=8,(m∈R).(1)若曲线Γ是焦点为F1(-2,0),F2(2,0)的双曲线,求实数m的值;
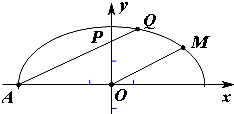
(2)当m=4时,记M是椭圆Γ上的动点,过椭圆长轴的端点A作AQ∥QM(O为坐标原点),交椭圆于Q,交y轴于P,求
| AQ•AP |
| OM2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)曲线Γ化为标准方程得
-
=1,由此利用双曲线的简单性质能求出m的值.
(2)当m=4时,曲线Γ:x2+2y2=8,此时A(-2
,0),由
,得:x2=
,由此利用韦达定理结合题设条件能求出
的值.
| x2 | ||
|
| y2 | ||
|
(2)当m=4时,曲线Γ:x2+2y2=8,此时A(-2
| 2 |
|
| 8 |
| 1+2k2 |
| AQ•AP |
| OM2 |
解答:
解:(1)∵曲线Γ:(5-m)x2+(m-2)y2=8,(m∈R),
化简得
-
=1,…(2分)
由题意得a2=
,b2=
,且m<2,…(3分)
又∵c=2,∴
+
=4,解得m=-1,或m=4(舍)…(5分)
∴m=-1.…(6分)
(2)当m=4时,曲线Γ:x2+2y2=8,此时A(-2
,0),…(7分)
设直线OM方程为y=kx,
由
,得:x2=
,
即xM2=
,…(8分)
∴OM2=xM2+yM2=xM2+(kxM)2=
,…(10分)
∵AQ∥OM,∴AQ方程为:y=k(x+2
),
于是P(o,2
k),AP=
=2
•
,…(11分)
由
,得:(1+2k2)x2+8
k2x+16k2-8=0,
从而AQ=
•
=
•
.…(13分)
∴
=
=2.…(14分)
化简得
| x2 | ||
|
| y2 | ||
|
由题意得a2=
| 8 |
| 5-m |
| 8 |
| 2-m |
又∵c=2,∴
| 8 |
| 5-m |
| 8 |
| 2-m |
∴m=-1.…(6分)
(2)当m=4时,曲线Γ:x2+2y2=8,此时A(-2
| 2 |
设直线OM方程为y=kx,
由
|
| 8 |
| 1+2k2 |
即xM2=
| 8 |
| 1+2k2 |
∴OM2=xM2+yM2=xM2+(kxM)2=
| 8(1+k2) |
| 1+2k2 |
∵AQ∥OM,∴AQ方程为:y=k(x+2
| 2 |
于是P(o,2
| 2 |
(-2
|
| 2 |
| 1+k2 |
由
|
| 2 |
从而AQ=
| 1+k2 |
| ||||
| 1+2k2 |
=
| 1+k2 |
4
| ||
| 1+2k2 |
∴
| AQ•AP |
| OM2 |
| ||||||||||
|
点评:本题考查双曲线中参数的求法,考查椭圆中线段比值的求法,综合性强,难度大,解题时要注意韦达定理的合理运用.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
一只蚂蚁在三边长分别为3,4,5的三角形内爬行,则此蚂蚁距离三角形三个顶点的距离均超过1的概率为( )
A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
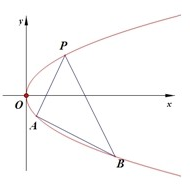 如图,抛物线的方程为y2=2px(p>0).
如图,抛物线的方程为y2=2px(p>0).