题目内容
在△ABC中,“sinA>sinB”是“A>B” 的条件.
考点:必要条件、充分条件与充要条件的判断
专题:计算题
分析:由正弦定理知
=
,由sinA>sinB,知a>b,所以A>B,反之亦然,故可得结论.
| a |
| sinA |
| b |
| sinB |
解答:
解:若sinA>sinB成立,
由正弦定理
=
=2R,
所以a>b,
所以A>B.
反之,若A>B成立,
所以a>b,
因为a=2RsinA,b=2RsinB,
所以sinA>sinB,
所以sinA>sinB是A>B的充要条件.
故答案为:充要条件.
由正弦定理
| a |
| sinA |
| b |
| sinB |
所以a>b,
所以A>B.
反之,若A>B成立,
所以a>b,
因为a=2RsinA,b=2RsinB,
所以sinA>sinB,
所以sinA>sinB是A>B的充要条件.
故答案为:充要条件.
点评:本题以三角形为载体,考查四种条件,解题的关键是正确运用正弦定理及变形.属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知{an}为等比数列,且a4+a7=2,a5a6=-8,则a1+a10=( )
| A、5 | B、-5 | C、7 | D、-7 |
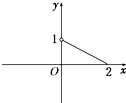 已知定义在[-2,2]上的奇函数f(x)在(0,2]上的图象如图所示,
已知定义在[-2,2]上的奇函数f(x)在(0,2]上的图象如图所示,