题目内容
已知函数f(x)=sin2x+
sinxcosx-1.
(1)求函数的最小正周期;
(2)当x∈[-
,
]时,求函数f(x)的值域.
| 3 |
(1)求函数的最小正周期;
(2)当x∈[-
| π |
| 12 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:计算题,三角函数的图像与性质
分析:(1)利用三角函数中的恒等变换可求得f(x)=sin(2x-
)-
,从而可求得其最小正周期;
(2)x∈[-
,
]⇒2x-
[-
,
]⇒sin(2x-
)∈[-
,1],从而可求得函数f(x)的值域.
| π |
| 6 |
| 1 |
| 2 |
(2)x∈[-
| π |
| 12 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
| ||
| 2 |
解答:
解:(1)∵f(x)=sin2x+
sinxcosx-1
=
+
sin2x-1
=
sin2x-
cos2x-
=sin(2x-
)-
,
∴函数f(x)=sin2x+
sinxcosx-1的最小正周期T=
=π;
(2)∵x∈[-
,
],
∴2x-
[-
,
],
∴sin(2x-
)∈[-
,1],
∴f(x)∈[-
,
].
| 3 |
=
| 1-cos2x |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
| 1 |
| 2 |
∴函数f(x)=sin2x+
| 3 |
| 2π |
| 2 |
(2)∵x∈[-
| π |
| 12 |
| π |
| 2 |
∴2x-
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
∴sin(2x-
| π |
| 6 |
| ||
| 2 |
∴f(x)∈[-
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查三角函数中的恒等变换,考查正弦函数的周期性与单调性,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
圆C1:(x-1)2+y2=1与圆C2:x2+(y-2)2=4的位置关系是( )
| A、相交 | B、相离 | C、外切 | D、内切 |
已知△ABC外接圆的半径为1,圆心为O.若|
|=|
|,且2
+
+
=0,则
•
等于( )
| OA |
| AB |
| OA |
| AB |
| AC |
| CA |
| CB |
A、
| ||
B、2
| ||
C、
| ||
| D、3 |
在圆(x-3)2+(y-5)2=2的切线中,满足在两坐标轴上截距相等的直线共有( )
| A、2条 | B、3条 | C、4条 | D、5条 |
已知向量
=(4-x,1),
=(y,x+5),x,y∈(0,+∞),且
⊥
,则xy取得最小值时,x=( )
| a |
| b |
| a |
| b |
| A、3 | ||
| B、1 | ||
| C、2 | ||
D、
|
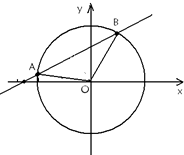 已知直线l:y=k(x+2
已知直线l:y=k(x+2