题目内容
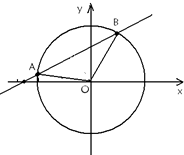 已知直线l:y=k(x+2
已知直线l:y=k(x+2| 2 |
(1)求k的取值范围;
(2)三角形ABO的面积为S,试将S表示成k的函数,并求出它的定义域;
(3)求S的最大值,并求取得最大值时k的值.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)三点A、B、O构成三角形,则0<
<2,从而可求k的取值范围;
(2)求出|AB|,表示出三角形的面积,即可得到S表示成k的函数;
(3)换元,利用配方法,即可求S的最大值.
2
| ||
|
(2)求出|AB|,表示出三角形的面积,即可得到S表示成k的函数;
(3)换元,利用配方法,即可求S的最大值.
解答:
 解:(1)由题意,dOM=
解:(1)由题意,dOM=
,
∵三点A、B、O构成三角形,
∴0<
<2,
∴-1<k<1且k≠0;
(2)直线l:y=k(x+2
),即kx-y+2
k=0,
∴dOM=
,
∴|AB|=2
=4
,
∴S=
|AB|dOM=
•=4
•
=
(-1<k<1且k≠0);
(3)设k2+1=t(t≥1),则S=4
•
=4
•
,
∴
=
,即t=
时,k=±
,Smax=4
•
=2,
∴S的最大值为2,取得最大值时k=±
.
 解:(1)由题意,dOM=
解:(1)由题意,dOM=2
| ||
|
∵三点A、B、O构成三角形,
∴0<
2
| ||
|
∴-1<k<1且k≠0;
(2)直线l:y=k(x+2
| 2 |
| 2 |
∴dOM=
2
| ||
|
∴|AB|=2
4-(
|
|
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
|
2
| ||
|
4
| ||||
| 1+k2 |
(3)设k2+1=t(t≥1),则S=4
| 2 |
| ||
| t |
| 2 |
-2(
|
∴
| 1 |
| t |
| 3 |
| 4 |
| 4 |
| 3 |
| ||
| 3 |
| 2 |
| 1 | ||
2
|
∴S的最大值为2,取得最大值时k=±
| ||
| 3 |
点评:本题考查点到直线的距离公式的运用,考查三角形面积的计算,考查换元法、配方法,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
若x2+y2=100,则直线4x-3y+50=0与圆的位置关系是( )
| A、相交 | B、相离 |
| C、相切 | D、相交但不过圆心 |
已知空间上的两点A(-1,2,1)、B(-2,0,3),以AB为体对角线构造一个正方体,则该正方体的体积为( )
| A、3 | ||
B、2
| ||
| C、9 | ||
D、3
|
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )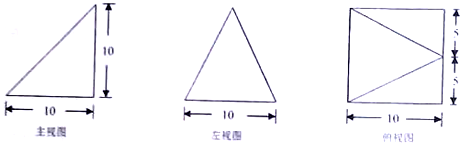

A、
| ||
B、
| ||
| C、1000cm3 | ||
| D、2000cm3 |
 如图,椭圆
如图,椭圆