题目内容
 如图,已知PA⊥面ABCD,PA=AB=AD=
如图,已知PA⊥面ABCD,PA=AB=AD=| 1 |
| 2 |
(1)在线段PC上找一点M,使BM⊥面PCD.
(2)求由面PBC与面PAD所成角的二面角的正切值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)令M为PC的中点,设PD中点为N,通过证明BM∥AN,AN⊥面PCD,即可在线段PC上找一点M,使BM⊥面PCD.
(2)延长CB交DA于E,说明∠CPD为二面角C-PE-D的平面角,在△PCD中,求由面PBC与面PAD所成角的二面角的正切值.
(2)延长CB交DA于E,说明∠CPD为二面角C-PE-D的平面角,在△PCD中,求由面PBC与面PAD所成角的二面角的正切值.
解答:
解:(1)M为PC的中点,设PD中点为N,
则MN=
CD,且MN∥
CD,∴MN=AB,MN∥AB
∴ABMN为平行四边形,∴BM∥AN,
又PA=AD,∠PAD=90°
∴AN⊥PD,
又CD⊥AN,∴AN⊥面PCD,
∴BM⊥面PCD,
(2)延长CB交DA于E,
∵AB=
CD.AB∥
CD
∴AE=AD=PA,∴PD⊥PE
又∴PE⊥CD,∴PE⊥面PCD,
∴∠CPD为二面角C-PE-D的平面角;
在△PCD中,PD=
AD,CD=2AD;
∴tan∠CPD=
.
则MN=
| 1 |
| 2 |
| 1 |
| 2 |
∴ABMN为平行四边形,∴BM∥AN,
又PA=AD,∠PAD=90°
∴AN⊥PD,
又CD⊥AN,∴AN⊥面PCD,
∴BM⊥面PCD,
(2)延长CB交DA于E,
∵AB=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=AD=PA,∴PD⊥PE
又∴PE⊥CD,∴PE⊥面PCD,
∴∠CPD为二面角C-PE-D的平面角;
在△PCD中,PD=
| 2 |
∴tan∠CPD=
| 2 |
点评:本题考查空间直线与平面垂直,二面角的求法,考查空间想象能力、逻辑推理能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
复数
的虚部是( )
| 2+i |
| 1-i |
A、-
| ||
B、
| ||
C、
| ||
D、
|
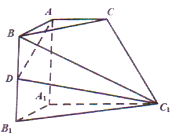 如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.
如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.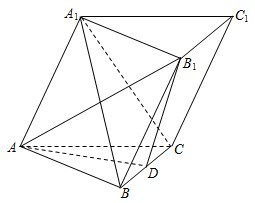 在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥平面ABC,∠ACB=90°,D为BC中点.
在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥平面ABC,∠ACB=90°,D为BC中点. 如图,在三棱柱ABC-A1B1C1中,AB=AC,侧棱与底面垂直,点D是棱BC的中点.
如图,在三棱柱ABC-A1B1C1中,AB=AC,侧棱与底面垂直,点D是棱BC的中点.