题目内容
若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)-g(x)=x-1,则有( )
| A、f(2)<f(3)<g(0) |
| B、g(0)<f(3)<f(2) |
| C、f(2)<g(0)<f(3) |
| D、g(0)<f(2)<f(3) |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:利用函数的奇偶性、函数的单调性即可得出.
解答:
解:∵函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)-g(x)=x-1.
∴f(-x)-g(-x)=-x-1,即-f(x)-g(x)=-x-1,化为f(x)+g(x)=x+1.
联立
,解得f(x)=x,g(x)=1.
∴g(0)=1,f(2)=2,f(3)=3.
∴g(0)<f(2)<f(3).
故选:D.
∴f(-x)-g(-x)=-x-1,即-f(x)-g(x)=-x-1,化为f(x)+g(x)=x+1.
联立
|
∴g(0)=1,f(2)=2,f(3)=3.
∴g(0)<f(2)<f(3).
故选:D.
点评:本题考查了函数的奇偶性、函数的单调性,属于基础题.

练习册系列答案
相关题目
若F(5,0)是双曲线
-
=1(m是常数)的一个焦点,则m的值为( )
| x2 |
| 16 |
| y2 |
| m |
| A、3 | B、5 | C、7 | D、9 |
如果b<a<0,那么下列不等式错误的是( )
| A、c+b<c+a | ||||
| B、a2<b2 | ||||
| C、bc2<ac2 | ||||
D、
|
已知向量
=(sinωx,cosωx),
=(cosωx,cosωx),其中ω>0,函数f (x)=2
•
-1的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)求函数f (x)在[
,
]上的取值范围.
| m |
| n |
| m |
| n |
(Ⅰ)求ω的值;
(Ⅱ)求函数f (x)在[
| π |
| 4 |
| 3π |
| 4 |
| C | 2 6 |
| A、4 | B、8 | C、10 | D、15 |
以下给出的各数中不可能是八进制数的是( )
| A、231 | B、10110 |
| C、82 | D、4757 |
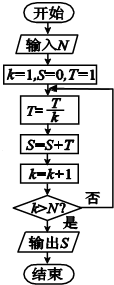 阅读如图的程序框图,解答以下问题:
阅读如图的程序框图,解答以下问题: