题目内容
已知平面直角坐标内的向量
=(1,3),
=(m,2m-3),若该平面内不是所有的向量都能写成x
+y
(x,y∈R)的形式,则m的值为( )
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
| C、-3 | ||
| D、3 |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:根据平面向量的基本定理得出向量
、
共线,从而求出m的值.
| a |
| b |
解答:
解:根据题意,得向量
、
共线,
∴1×(2m-3)-3m=0,
解得m=-3.
故选:C.
| a |
| b |
∴1×(2m-3)-3m=0,
解得m=-3.
故选:C.
点评:本题考查了平面向量的应用问题,解题的关键是由题意得出向量
、
共线,是基础题.
| a |
| b |

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
若数列{an}满足
-
=0,n∈N*,p为非零常数,则称数列{an}为“梦想数列”.已知正项数列{
}为“梦想数列”,且b1b2b3…b99=299,则b8+b92的最小值是( )
| 1 |
| an+1 |
| p |
| an |
| 1 |
| bn |
| A、2 | B、4 | C、6 | D、8 |
设等差数列{an}的前n项和为Sn且满足S15>0,S16<0则
,
,
,…,
中最大的项为( )
| S1 |
| a1 |
| S2 |
| a2 |
| S3 |
| a3 |
| S15 |
| a15 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若F(5,0)是双曲线
-
=1(m是常数)的一个焦点,则m的值为( )
| x2 |
| 16 |
| y2 |
| m |
| A、3 | B、5 | C、7 | D、9 |
设函数f(x)=
+a是奇函数(a为常数),则f(x)<0的解集为( )
| 1 |
| 2x+1 |
| A、(0,+∞) | ||
| B、(1,+∞) | ||
| C、(-1,0)∪(0,1) | ||
D、(
|
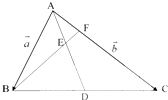 在△ABC中,D是BC中点,线段AD上的点E满足
在△ABC中,D是BC中点,线段AD上的点E满足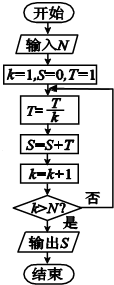 阅读如图的程序框图,解答以下问题:
阅读如图的程序框图,解答以下问题: