题目内容
复数z=（1-i）a2-3a+2+i（a∈R），
（1）若z=
，求|z|；
（2）若在复平面内复数z对应的点在第一象限，求a的范围．
（1）若z=
. |
| z |
（2）若在复平面内复数z对应的点在第一象限，求a的范围．
考点：复数求模,复数的基本概念
专题：数系的扩充和复数
分析：（1）根据z=
，确定方程即可求|z|；
（2）利用复数的几何意义，即可得到结论．
. |
| z |
（2）利用复数的几何意义，即可得到结论．
解答：
解 z=（1-i）a2-3a+2+i=a2-3a+2+（1-a2）i，
（1）由z=
知，1-a2=0，故a=±1．
当a=1时，z=0；
当a=-1时，z=6．
（2）由已知得，复数的实部和虚部皆大于0，
即
，
即
，
所以-1＜a＜1．
（1）由z=
. |
| z |
当a=1时，z=0；
当a=-1时，z=6．
（2）由已知得，复数的实部和虚部皆大于0，
即
|
即
|
所以-1＜a＜1．
点评：本题主要考查复数的几何意义，以及复数的有关概念，比较基础．
练习册系列答案
名题金卷系列答案
相关题目
若实数x，y满足
，则z=2x+2y的最小值是（ ）
|
| A、0 | ||
| B、1 | ||
C、
| ||
| D、9 |
如图所示，在三棱锥P-ABC中，E、F分别为AC、BC的中点．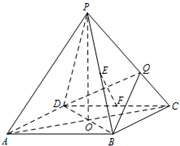
如图，正四棱锥P-ABCD的高为PO，PO=AB=2．E，F分别是棱PB，CD的中点，Q是棱PC上的点．
如图，△ABC内接于⊙O，AB=AC，点D在⊙O上，AD⊥AB，AD交BC于点E，点F在DA的延长线上，AF=AE，求证：