题目内容
已知函数f(x)=x3+x2-ax(a∈R).
(1)当a=0时,求与直线x-y-10=0平行,且与曲线y=f(x)相切的直线的方程;
(2)求函数g(x)=
-alnx(x>1)的单调递增区间;
(3)如果存在a∈[3,9],使函数h(x)=f(x)+f′(x)(x∈[-3,b])在x=-3处取得最大值,试求b的最大值.
(1)当a=0时,求与直线x-y-10=0平行,且与曲线y=f(x)相切的直线的方程;
(2)求函数g(x)=
| f(x) |
| x |
(3)如果存在a∈[3,9],使函数h(x)=f(x)+f′(x)(x∈[-3,b])在x=-3处取得最大值,试求b的最大值.
考点:利用导数研究函数的单调性,利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)根据导数与函数切线斜率的关系,求得斜率,由点斜式写出切线方程;
(2)利用导数判断函数的单调性求得函数的单调递增区间即可;
(3)利用导数求函数的最值的方法,通过分类讨论得出b的最大值.
(2)利用导数判断函数的单调性求得函数的单调递增区间即可;
(3)利用导数求函数的最值的方法,通过分类讨论得出b的最大值.
解答:
解:(1)设切点为T(x0,x03+x02),由f′(x)=3x2+2x及题意
得3 x02+2 x0=1. …(2分)
解得x0=-1,或x0=
.
所以T(-1,0)或T(
,
).
所以切线方程为x-y+1=0或27x-27y-5=0. …(4分)
(2)因为g(x)=x2+x-a-alnx(x>1),
所以由g′(x)=2x+1-
>0,得2x2+x-a>0. …(6分)
令φ(x)=2x2+x-a(x>1),因为φ(x)在(1,+∞)递增,所以φ(x)>φ(1)=3-a.
当3-a≥0即a≤3时,g(x)的增区间为(1,+∞); …(8分)
当3-a<0即a>3时,
因为φ(1)=3-a<0,所以φ(x)的一个零点小于1、另一个零点大于1.
由φ(x)=0得零点x1=
<1,x2=
>1,
从而φ(x)>0(x>1)的解集为(
,+∞),
即g(x)的增区间为(
,+∞). …(10分)
(3)方法一:h(x)=x3+4x2+(2-a)x-a,h′(x)=3x2+8x+(2-a).
因为存在a∈[3,9],令h′(x)=0,得x1=
,x2=
.
当x<x1或x>x2时,h′(x)>0;当x1<x<x2时,h′(x)<0.
所以要使h(x)(x∈[-3,b])在x=-3处取得最大值,
必有
解得a≥5,即a∈[5,9]. …(13分)
所以存在a∈[5,9]使h(x)(x∈[-3,b])在x=-3处取得最大值的充要条件为h(-3)≥h(b),
即存在a∈[5,9]使(b+3)a-(b3+4b2+2b-3)≥0成立.
因为b+3>0,所以9(b+3)-(b3+4b2+2b-3)≥0,即(b+3)( b2+b-10)≤0.
解得
≤b≤
,所以b的最大值为
. …(16分)
方法二:h(x)=x3+4x2+(2-a)x-a,
据题意知,h(x)≤h(-3)在区间[-3,b]上恒成立.
即(x3+27)+4(x2-9)+(2-a)(x+3)≤0,(x+3)(x2+x-1-a)≤0 ①.
若x=-3时,不等式①成立;
若-3<x≤b时,不等式①可化为x2+x-1-a≤0,即x2+x≤1+a ②.…(13分)
令ψ(x)=x2+x.
当-3<b≤2时,ψ(x)在区间[-3,b]上的最大值为ψ(-3)=6,
不等式②恒成立等价于6≤1+a,a≥5,符合题意;
当b≥2时,ψ(x)的最大值为ψ(b)=b2+b,不等式②恒成立等价于b2+b≤1+a.
由题意知这个关于a的不等式在区间[3,9]上有解.
故b2+b≤(1+a)max,即b2+b≤10,b2+b-10≤0,解得2<b≤
.
综上所述,b的最大值为
,此时唯有a=9符合题意.…(16分)
得3 x02+2 x0=1. …(2分)
解得x0=-1,或x0=
| 1 |
| 3 |
所以T(-1,0)或T(
| 1 |
| 3 |
| 4 |
| 27 |
所以切线方程为x-y+1=0或27x-27y-5=0. …(4分)
(2)因为g(x)=x2+x-a-alnx(x>1),
所以由g′(x)=2x+1-
| a |
| x |
令φ(x)=2x2+x-a(x>1),因为φ(x)在(1,+∞)递增,所以φ(x)>φ(1)=3-a.
当3-a≥0即a≤3时,g(x)的增区间为(1,+∞); …(8分)
当3-a<0即a>3时,
因为φ(1)=3-a<0,所以φ(x)的一个零点小于1、另一个零点大于1.
由φ(x)=0得零点x1=
-1-
| ||
| 4 |
-1+
| ||
| 4 |
从而φ(x)>0(x>1)的解集为(
-1+
| ||
| 4 |
即g(x)的增区间为(
-1+
| ||
| 4 |
(3)方法一:h(x)=x3+4x2+(2-a)x-a,h′(x)=3x2+8x+(2-a).
因为存在a∈[3,9],令h′(x)=0,得x1=
-4-
| ||
| 3 |
-4+
| ||
| 3 |
当x<x1或x>x2时,h′(x)>0;当x1<x<x2时,h′(x)<0.
所以要使h(x)(x∈[-3,b])在x=-3处取得最大值,
必有
|
所以存在a∈[5,9]使h(x)(x∈[-3,b])在x=-3处取得最大值的充要条件为h(-3)≥h(b),
即存在a∈[5,9]使(b+3)a-(b3+4b2+2b-3)≥0成立.
因为b+3>0,所以9(b+3)-(b3+4b2+2b-3)≥0,即(b+3)( b2+b-10)≤0.
解得
-1-
| ||
| 2 |
-1+
| ||
| 2 |
-1+
| ||
| 2 |
方法二:h(x)=x3+4x2+(2-a)x-a,
据题意知,h(x)≤h(-3)在区间[-3,b]上恒成立.
即(x3+27)+4(x2-9)+(2-a)(x+3)≤0,(x+3)(x2+x-1-a)≤0 ①.
若x=-3时,不等式①成立;
若-3<x≤b时,不等式①可化为x2+x-1-a≤0,即x2+x≤1+a ②.…(13分)
令ψ(x)=x2+x.
当-3<b≤2时,ψ(x)在区间[-3,b]上的最大值为ψ(-3)=6,
不等式②恒成立等价于6≤1+a,a≥5,符合题意;
当b≥2时,ψ(x)的最大值为ψ(b)=b2+b,不等式②恒成立等价于b2+b≤1+a.
由题意知这个关于a的不等式在区间[3,9]上有解.
故b2+b≤(1+a)max,即b2+b≤10,b2+b-10≤0,解得2<b≤
-1+
| ||
| 2 |
综上所述,b的最大值为
-1+
| ||
| 2 |
点评:本题主要考查利用导数研究函数的切线方程、判断函数的单调性、求函数最值等知识,考查分类讨论思想的运用能力,综合性强,属难题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点.
如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点.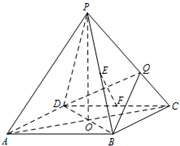 如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点.
如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点.