题目内容
已知向量 ,向量
,向量 ,函数
,函数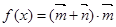 .
.
(1)求 的最小正周期
的最小正周期 ;
;
(2)已知 分别为
分别为 内角
内角 的对边,
的对边, 为锐角,
为锐角,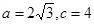 ,且
,且 恰是
恰是 在
在 上的最大值,求
上的最大值,求 和
和 .
.
(1)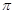 ;(2)
;(2)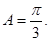
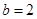
解析试题分析:(1)首先根据向量和的坐标运算和向量数量积的坐标表示将函数 的解析式化为
的解析式化为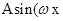
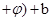 的形式,再利用
的形式,再利用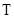 和
和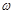 的关系求周期;(2)先根据
的关系求周期;(2)先根据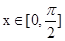 确定
确定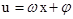 的取值范围,再结合
的取值范围,再结合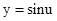 的图像求出
的图像求出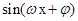 的范围,进而求
的范围,进而求 在
在 上的最大值即
上的最大值即 ,进而确定
,进而确定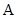 ,此时三角形知道两边和其中一边的对角,利用余弦定理列关于
,此时三角形知道两边和其中一边的对角,利用余弦定理列关于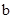 的方程,解之即可.
的方程,解之即可.
试题解析:(1)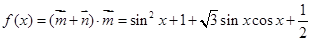 ,
,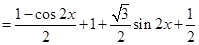
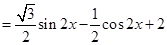
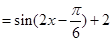 ,
,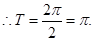
(2)由(1)知: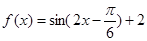 ,
,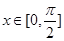 时,
时,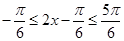
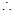 当
当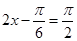 时
时 取得最大值
取得最大值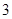 ,此时
,此时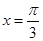 .
. 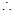 由
由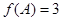 得
得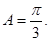
由余弦定理,得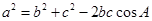 ∴
∴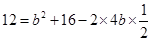 , ∴
, ∴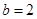 .
.
考点:1、向量的线性运算和数量积运算;2、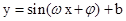 型函数的值域;3、余弦定理.
型函数的值域;3、余弦定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,每批游客从各自报名点到C岛所需运输成本S元。
,每批游客从各自报名点到C岛所需运输成本S元。
 的函数表达式,并指出
的函数表达式,并指出 ,
, ,其中ω>0,函数
,其中ω>0,函数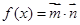 ,若
,若 相邻两对称轴间的距离为
相邻两对称轴间的距离为 .
. ,△ABC的面积S=5
,△ABC的面积S=5 ,b=4,,求a.
,b=4,,求a. 中,角A、B,C,所对的边分别为
中,角A、B,C,所对的边分别为 ,且
,且
 的值;
的值; ,求
,求 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
. 的值;
的值; ,且
,且 ,求
,求 和
和 的值.
的值. 中,角
中,角 的对边分别为
的对边分别为 .已知
.已知 .
. ;
; ,
, ,且
,且 ,求
,求 .
. ,设函数
,设函数 +1
+1 ,
,  ,求
,求 的值;
的值; ,且满足
,且满足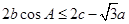 ,求
,求
 的最大值为2.
的最大值为2. 在
在 上的单调递减区间;
上的单调递减区间; 中,
中, ,角
,角 所对的边分别是
所对的边分别是 ,且
,且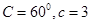 ,求
,求 中,其中
中,其中 为定点,
为定点, 为动点,满足
为动点,满足 .
. 与
与 的关系式;
的关系式; 的面积分别为
的面积分别为 和
和 ,求
,求 的最大值,以及此时凸四边形
的最大值,以及此时凸四边形