题目内容
 中,角
中,角 的对边分别为
的对边分别为 .已知
.已知 .
.
(I)求 ;
;
(II)若 ,
, 的面积为
的面积为 ,且
,且 ,求
,求 .
.
(I)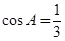 ;(II)
;(II) .
.
解析试题分析:(I)在 中,有差角
中,有差角 ,有单角
,有单角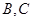 ,所以应将
,所以应将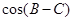 展开,将角统一为单角.
展开,将角统一为单角.
由 得:
得: ,
,
再移项合并得: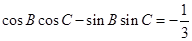 ,这样可得
,这样可得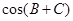 的值,从而求出
的值,从而求出 的值.
的值.
(II)面积公式用哪一个?因为由(I)可得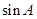 ,所以用
,所以用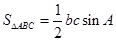 ,由此可得
,由此可得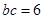 …①
…①
为了求出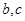 ,显然还应该再找一个含
,显然还应该再找一个含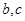 的等式.
的等式.
因为已知 ,在(I)题中又求出了
,在(I)题中又求出了 ,所以可用余弦定理再得一个含
,所以可用余弦定理再得一个含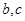 的等式:
的等式: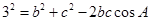 ……………………………………………②
……………………………………………②
这样联立①②便可求出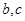 的值.
的值.
试题解析:(I)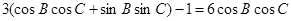 ,
, .
.
(II)由(I)得 ,由面积
,由面积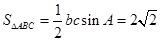 可得:
可得: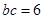 ………………①
………………①
因为 ,所以由余弦定理得:
,所以由余弦定理得: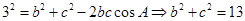 ………………………②
………………………②
联立①②得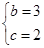 或
或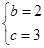 (舍).
(舍).
综上: .
.
考点:1、三角恒等变换;2、余弦定理;3、三角形的面积;4、解方程组.

练习册系列答案
相关题目
 两个小岛相距10
两个小岛相距10 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至 处进行作业,且
处进行作业,且 .设
.设

 分别表示
分别表示 和
和 ,并求出
,并求出 的距离为
的距离为 ,求BD的最大值.
,求BD的最大值. 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
, .
. 的值;
的值; 的值.
的值. 中,角
中,角 的对边分别为
的对边分别为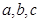 ,且
,且 .
.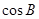 的值;
的值; ,且
,且 ,求
,求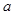 和
和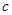 的值.
的值. ,向量
,向量 ,函数
,函数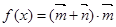 .
. 的最小正周期
的最小正周期 ;
; 分别为
分别为 内角
内角 的对边,
的对边, 为锐角,
为锐角,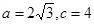 ,且
,且 恰是
恰是 上的最大值,求
上的最大值,求 .
. 中,
中,
 的值;
的值; 的值.
的值.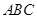 中,内角
中,内角 所对的边分别为
所对的边分别为 ,已知m
,已知m ,n
,n ,m·n
,m·n .
. 的大小;
的大小; ,
, ,求△
,求△ 中,角
中,角 的对边分别为
的对边分别为 ,
, 。
。 的值;(Ⅱ)求
的值;(Ⅱ)求 ,求B.
,求B.