题目内容
14.函数y=$\left\{\begin{array}{l}{|cosx|,x>1}\\{0,x≤1}\end{array}\right.$,则:f(1)=0;f($\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$;f(π)=1.分析 利用函数性质直接求解.
解答 解:∵函数y=$\left\{\begin{array}{l}{|cosx|,x>1}\\{0,x≤1}\end{array}\right.$,
∴f(1)=0,
f($\frac{π}{6}$)=|cos$\frac{π}{6}$|=$\frac{\sqrt{3}}{2}$,
f(π)=|cosπ|=1.
故答案为:0;$\frac{\sqrt{3}}{2}$;1.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
5.函数f(x)在(0,+∞)上为增函数,则不等式f(x)>f(8x-16)的解集为( )
| A. | (2,$\frac{16}{7}$) | B. | (-∞,2) | C. | ($\frac{16}{7}$,+∞) | D. | (2,+∞) |
19.已知f(x)=$\left\{\begin{array}{l}{2x+3,x<0}\\{2{x}^{2}+1,x≥0}\end{array}\right.$,则f[f(-1)]的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
3.根据如图框图,当输入x为9时,输出的y=( )


| A. | 1 | B. | 2 | C. | 5 | D. | 10 |
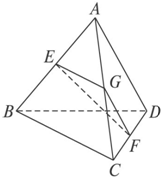 如图,点A是BCD所在平面外一点,AD=BC,E、F分别是 AB、CD的中点,且EF=$\frac{{\sqrt{2}}}{2}$AD,求异面直线AD和BC所成的角.
如图,点A是BCD所在平面外一点,AD=BC,E、F分别是 AB、CD的中点,且EF=$\frac{{\sqrt{2}}}{2}$AD,求异面直线AD和BC所成的角.