题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{{x}^{2}+2,x>0}\end{array}\right.$,则f(f(-1))的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先求出f(-1)=-(-1)=1,从而f(f(-1))=f(1),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{{x}^{2}+2,x>0}\end{array}\right.$,
∴f(-1)=-(-1)=1,
f(f(-1))=f(1)=12+2=3.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
3.函数y=sin2x-4sinx+1的值域为( )
| A. | [-5,-2] | B. | [-5,6] | C. | [-2,2] | D. | [-2,6] |
8.612,840,468的最大公约数为( )
| A. | 2 | B. | 4 | C. | 12 | D. | 24 |
5.函数f(x)在(0,+∞)上为增函数,则不等式f(x)>f(8x-16)的解集为( )
| A. | (2,$\frac{16}{7}$) | B. | (-∞,2) | C. | ($\frac{16}{7}$,+∞) | D. | (2,+∞) |
3.根据如图框图,当输入x为9时,输出的y=( )


| A. | 1 | B. | 2 | C. | 5 | D. | 10 |
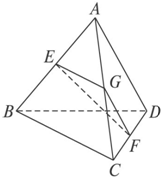 如图,点A是BCD所在平面外一点,AD=BC,E、F分别是 AB、CD的中点,且EF=$\frac{{\sqrt{2}}}{2}$AD,求异面直线AD和BC所成的角.
如图,点A是BCD所在平面外一点,AD=BC,E、F分别是 AB、CD的中点,且EF=$\frac{{\sqrt{2}}}{2}$AD,求异面直线AD和BC所成的角.