题目内容
在三角形△ABC所在的平面上有一点P,满足6
=3
+2
,则△PBC与△ABC的面积之比是( )
| AP |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:向量在几何中的应用
专题:计算题,平面向量及应用
分析:由6
=3
+2
,可得
=
+
,从而P到BC的距离是A到BC距离的
,即可得出△PBC与△ABC的面积之比.
| AP |
| AB |
| AC |
| BP |
| 1 |
| 6 |
| BA |
| 1 |
| 3 |
| BC |
| 1 |
| 6 |
解答:
解:∵6
=3
+2
,∴6(
-
)=-3
+2(
-
),
∴
=
+
,
令
=
,
=
,则
=
+
∴四边形BDPE是平行四边形,
∴P到BC的距离是A到BC距离的
,
∴△PBC与△ABC的面积之比是
,
故选:A.
| AP |
| AB |
| AC |
| BP |
| BA |
| BA |
| BC |
| BA |
∴
| BP |
| 1 |
| 6 |
| BA |
| 1 |
| 3 |
| BC |
令
| BE |
| 1 |
| 6 |
| BA |
| BD |
| 1 |
| 3 |
| BC |
| BP |
| BE |
| BD |
∴四边形BDPE是平行四边形,
∴P到BC的距离是A到BC距离的
| 1 |
| 6 |
∴△PBC与△ABC的面积之比是
| 1 |
| 6 |
故选:A.
点评:本题考查向量知识的运用,考查三角形面积比,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
在△ABC中,a,b,c分别为角A,B,C所对的边,且b2+c2-
bc=3,cosB=
,a=
,则边c的值为( )
| 2 |
| 4 |
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等比数列{an}中,a2a4=16,则a1a5=( )
| A、4 | B、16 | C、-4 | D、-16 |
同时掷两颗骰子,得到点数和为8的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=loga|x-1|在(0,1)上递减,那么f(x)在(1,+∞)上( )
| A、递增且无最大值 |
| B、递减且无最小值 |
| C、递增且有最大值 |
| D、递减且有最小值 |
设a=∫
(sinx+cosx)dx,则二项式(a
-
)6展开式中各项系数之和是( )
π 0 |
| x |
| 1 | ||
|
| A、1 | B、-1 | C、2 | D、0 |
根据图所示程序框图,当输入10时,输出的是( )


| A、14.1 | B、19 |
| C、12 | D、-30 |
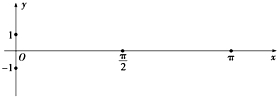 某简谐运动的图象对应的函数解析式为:y=
某简谐运动的图象对应的函数解析式为:y=