题目内容
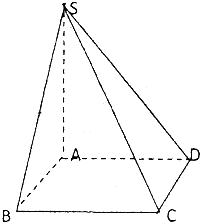（文） 如图，四棱锥S-ABCD中，底面ABCD为正方形，SA⊥平面ABCD，AB=3，SA=4（1）求异面直线SC与AD所成角；
（2）求点B到平面SCD的距离．
考点：点、线、面间的距离计算,异面直线及其所成的角
专题：计算题,空间位置关系与距离,空间角
分析：（1）由已知BC∥AD，∠SCB就是异面直线SC与AD所成角，由此能求出直线SC与AD所成角．
（2）利用等体积可求点B到平面SCD的距离．
（2）利用等体积可求点B到平面SCD的距离．
解答：
解：（1）∵BC∥AD，∴∠SCB就是异面直线SC与AD所成角，
∵SA⊥BC，BC⊥AB，SA∩AB=A，∴BC⊥平面SAB，
∴BC⊥SB，
Rt△SBC中，SB=5，BC=3，
∴tan∠SCB=
，
∴直线SC与AD所成角为arctan
．
（2）连接BD，设点B到平面SCD的距离为h．
∵VS-BCD=VB-SCD，
∴
S△BCD•SA=
S△SCDh，
∴
×4=
h，
∴h=
，
∴点B到平面SCD的距离为
．
∵SA⊥BC，BC⊥AB，SA∩AB=A，∴BC⊥平面SAB，
∴BC⊥SB，
Rt△SBC中，SB=5，BC=3，
∴tan∠SCB=
| 5 |
| 3 |
∴直线SC与AD所成角为arctan
| 5 |
| 3 |
（2）连接BD，设点B到平面SCD的距离为h．
∵VS-BCD=VB-SCD，
∴
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 9 |
| 2 |
| 15 |
| 2 |
∴h=
| 12 |
| 5 |
∴点B到平面SCD的距离为
| 12 |
| 5 |
点评：本题考查直线与直线所成角的求法，考查几何体的体积的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
若a＞0且a≠1，b＞0，则“logab＞0”是“（a一1）（b一1）＞0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在空间四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，对角线AC=BD=2，且AC⊥BD，则四边形EFGH的面积为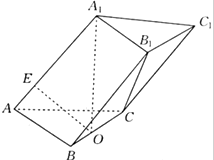
已知在三棱柱ABC-A1B1C1中，底面ABC为正三角形，A1在底面ABC上的射影是棱BC的中点O，OE⊥AA1于E点．已知f（1）=1，f（x）=
（x=2，3，…），m∈N+，则f（2m）=（ ）
|
| A、2m+1 | |||||
B、
| |||||
C、
| |||||
| D、3m2+2m |