题目内容
3.在△ABC中,a,b,c分别是角A,B,C的对边,已知(a-3b)cosC=c(3cosB-cosA).(1)求$\frac{sinB}{sinA}$的值;
(2)若c=$\sqrt{7}$a,求角C的大小.
分析 (1)利用正弦定理将边化角整理化简条件式子,得出sinA和sinB的关系;
(2)用a表示b,c,使用余弦定理求出cosC.
解答 解:(1)∵(a-3b)cosC=c(3cosB-cosA),
∴sinAcosC-3sinBcosC=3cosBsinC-cosAsinC,
即sinAcosC+cosAsinC=3cosBsinC+3sinBcosC,
∴sin(A+C)=3sin(B+C),即sinB=3sinA,
∴$\frac{sinB}{sinA}$=3.
(2)∵$\frac{sinB}{sinA}$=3,∴b=3a.
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{{a}^{2}+9{a}^{2}-7{a}^{2}}{6{a}^{2}}$=$\frac{1}{2}$.
∴C=$\frac{π}{3}$.
点评 本题考查了正弦定理,余弦定理解三角形,属于基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
13.已知M(x,y)是以A(-2,3),B(3,2)为端点的线段上一动点,则$\frac{y-1}{x+1}$的取值范围为( )
| A. | [-2,$\frac{1}{4}$] | B. | (-∞,-2] | C. | (-∞,2]∪[$\frac{1}{4}$,+∞) | D. | [$\frac{1}{4}$,+∞) |
18.在平面直角坐标系中,一束光线从点M(-2,3)出发,被直线y=x-1反射后到达点N(1,6),则这束光线从M到N所经过的路程为( )
| A. | 10$\sqrt{3}$ | B. | 3$\sqrt{10}$ | C. | 2$\sqrt{10}$ | D. | 3$\sqrt{2}$ |
 构造如图所示的数表,规则如下:先排两个1作为第一层,然后在每一层的相邻两个数之间插入这两个数和的a倍得下一层,其中a>0,设n层中有an个数,这an个数的和为Sn(n∈N*).
构造如图所示的数表,规则如下:先排两个1作为第一层,然后在每一层的相邻两个数之间插入这两个数和的a倍得下一层,其中a>0,设n层中有an个数,这an个数的和为Sn(n∈N*).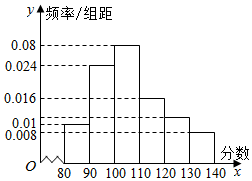 某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.
某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.