题目内容
10. 如图,在长方体ABCD-A1B1C1D1中,AB=2,AD=1,A1A=1,
如图,在长方体ABCD-A1B1C1D1中,AB=2,AD=1,A1A=1,(1)求证:直线BC1∥平面D1AC;
(2)求直线BC1到平面D1AC的距离.
分析 (1)根据线面平行的判定定理证明即可;(2)求出三棱锥D1-ABC的体积V,再△AD1C为底面的三棱锥B--AD1C的体积,从而求出线BC1到平面D1AC的距离即可.
解答  解:(1)因为ABCD-A1B1C1D1为长方体,故AB∥C1D1,AB=C1D1,
解:(1)因为ABCD-A1B1C1D1为长方体,故AB∥C1D1,AB=C1D1,
故ABC1D1为平行四边形,故BC1∥AD1,显然B不在平面D1AC上,
故 直线BC1平行于平面DA1C;
(2)直线BC1到平面D1AC的距离即为点B到平面D1AC的距离(设为h)
以△ABC为底面的三棱锥D1-ABC的体积V,可得V=$\frac{1}{3}×(\frac{1}{2}×1×2)×1=\frac{1}{3}$
而△AD1C中,AC=D1C=$\sqrt{5},A{D_1}=\sqrt{2}$,故${S_{△A{D_1}C}}$=$\frac{3}{2}$
所以以△AD1C为底面的三棱锥B--AD1C的体积V=$\frac{1}{3}×\frac{3}{2}×h=\frac{1}{3}⇒h=\frac{2}{3}$,
即直线BC1到平面D1AC的距离为$\frac{2}{3}$.
点评 本题考查了线面平行的判定定理,考查线面的距离以及数形结合思想,是一道中档题.

练习册系列答案
相关题目
15.已知正方体的不在同一表面的两个顶点A(-1,2,-1),B(3,-2,3),则正方体的棱长等于( )
| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
19.设f(x)是定义在(-π,0)∪(0,π)的奇函数,其导函数为f′(x),且$f({\frac{π}{2}})=0$,当x∈(0,π)时,f′(x)sinx-f(x)cosx<0,则关于x的不等式$f(x)<2f({\frac{π}{6}})sinx$的解集为( )
| A. | $({-\frac{π}{6},0})∪({0,\frac{π}{6}})$ | B. | $({-\frac{π}{6},0})∪({\frac{π}{6},π})$ | C. | $({-\frac{π}{6},0})∪({\frac{π}{6},\frac{π}{2}})$ | D. | $({-π,-\frac{π}{6}})∪({0,\frac{π}{6}})$ |
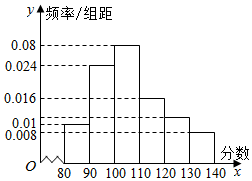 某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.
某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.