题目内容
11.已知sin(π+α)=$\frac{4}{5}$,则sin($\frac{π}{2}$+2α)=( )| A. | $\frac{7}{25}$ | B. | -$\frac{7}{25}$ | C. | -$\frac{24}{25}$ | D. | $\frac{24}{25}$ |
分析 已知等式利用诱导公式求出sinα的值,利用二倍角的三角函数公式求出cos2α的值,原式变形后代入计算即可求出值.
解答 解:∵sin(π+α)=-sinα=$\frac{4}{5}$,
∴sinα=-$\frac{4}{5}$,
则原式=cos2α=1-2sin2α=-$\frac{7}{25}$,
故选:B.
点评 此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
19.设f(x)是定义在(-π,0)∪(0,π)的奇函数,其导函数为f′(x),且$f({\frac{π}{2}})=0$,当x∈(0,π)时,f′(x)sinx-f(x)cosx<0,则关于x的不等式$f(x)<2f({\frac{π}{6}})sinx$的解集为( )
| A. | $({-\frac{π}{6},0})∪({0,\frac{π}{6}})$ | B. | $({-\frac{π}{6},0})∪({\frac{π}{6},π})$ | C. | $({-\frac{π}{6},0})∪({\frac{π}{6},\frac{π}{2}})$ | D. | $({-π,-\frac{π}{6}})∪({0,\frac{π}{6}})$ |
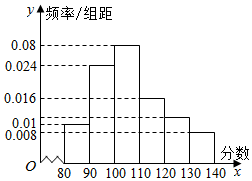 某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.
某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.
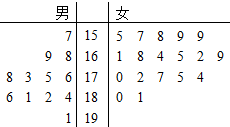 某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):